Простые числа и разложение на множители


Плюсануть
Поделиться
Класснуть
Запинить


Условие задачи Прогресс
ID 33571. Проверка на простоту
Темы: Простые числа и разложение на множители   

Проверьте, является ли число простым.

Входные данные 
Вводится одно натуральное число n не превышающее 2000000000 и не равное 1.

Выходные данные 
Необходимо вывести  строку prime, если число простое, или composite, если число составное.
 

Примеры
№ Входные данные Выходные данные
1 5 prime

ID 29549. Разложение на простые - 1
Темы: Простые числа и разложение на множители   

Требуется разложить целое число N на простые множители, представив его в виде произведения простых множителей и вывести результат в порядке возрастания.
 
Входные данные  
На вход падается число N (\(2 <= N <= 10^9\)).
 
Выходные данные 
Выведите список простых множителей числа N в порядке неубывания, разделенных знаком «*».
 
Примеры
№ Входные данные Выходные данные
1 5 5
2 30 2*3*5

ID 29548. Разложение на простые - 2
Темы: Простые числа и разложение на множители   

Требуется разложить целое число N на простые множители, представив его в виде произведения степеней простых множителей и вывести результат в порядке возрастания.
 
Входные данные 
На входе дано число N (\(2 <= N <= 10^9\)).
 
Выходные данные 
Вывести разложение N на простые множители.
 
Примеры
№ Входные данные Выходные данные
1 2 2
2 1008 2^4*3^2*7

ID 21767. Постулат Бертрана
Темы: Простые числа и разложение на множители   

Постулат Бертрана (теорема Бертрана-Чебышева, теорема Чебышева) гласит, что для любого \(n > 1\) найдется простое число p в интервале \(n < p < 2n\). Такая гипотеза была выдвинута в 1845 году французским математиком Джозефом Бертраном (проверившим ее до \(n=3000000\)) и доказана в 1850 году Пафнутием Чебышевым. Раманужан в 1920 году нашел более простое доказательство, а Эрдеш в 1932 – еще более простое.

Ваша задача состоит в том, чтобы решить несколько более общую задачу – а именно по числу n найти количество простых чисел p из интервала \(n < p < 2n\).

Напомним, что число называется простым, если оно делится только само на себя и на единицу

Входные данные
Целое число n (\(2 <= n <= 50000\)).

Выходные данные 
Выведите одно число – ответ на задачу.

 
Примеры
№ Входные данные Выходные данные
1 3000 353

ID 21768. Простые числа - 1
Темы: Простые числа и разложение на множители   

Найти количество всех четырехзначных простых чисел, оканчивающиеся на цифру k.

Входные данные 
Число k.

Выходные данные 
Вывести число - количество простых чисел, удовлетворяющих условию задачи. Если таких чисел нет то вывести слово Absent.


Примеры
№ Входные данные Выходные данные
1 1 266
2 0 Absent

ID 33572. Гипотеза Гольдбаха
Темы: Простые числа и разложение на множители   

Гипотеза Гольдбаха (не доказанная до сих пор) утверждает, что любое четное число (кроме 2) можно представить в виде суммы двух простых чисел.

Входные данные 
Программа получает на вход одно натуральное четное число n (\(3<n<2 \cdot 10^5\)).

Выходные данные 
Программа должна вывести два числа, разделенные пробелом. Числа должны быть простыми и давать в сумме n.
 

Примеры
№ Входные данные Выходные данные
1 4 2 2
2 6 3 3

ID 30756. Тройки чисел
Темы: Простые числа и разложение на множители   

Напишите программу, находящую количество троек целых чисел a, c, p таких, что p — простое число, числа удовлетворяют равенству: $$ \sqrt{a} - \sqrt{c} = \sqrt{p}. $$ Каждое из чисел a, c и p лежит в промежутке от N до M (то есть \(N<=a<= M,\ N<=c<= M,\ N<=p<= M\)).


Входные данные 
Вводятся два целых числа N и M (\(0<=N<=M<=100000\)).
 
Выходные данные 
Выведите искомое количество троек чисел a, c, p.
 
Примеры
№ Входные данные Выходные данные
1 1 8 1
2 5 20 1
3 1 7 0

ID 32949. Степень числа
Темы: Простые числа и разложение на множители   

Для заданного натурального A найти минимальное натуральное N такое, что N в степени N (N, умноженное на себя N раз) делится на A.
 
Входные данные 
На вход подается единственное число A (\(1 <= A <= 10^9\)).
 
Выходные данные
Необходимо вывести единственное число N.
 
Примеры
№ Входные данные Выходные данные
1 8 4
2 13 13

ID 30773. Простые числа - 2
Темы: Простые числа и разложение на множители   

Из заданного набора чисел выберите одно, имеющее максимальное количество простых делителей. Например, 30 имеет три простых делителя (2, 3 и 5), а 40 – только два (2 и 5).
 
Входные данные 
Первая строка  содержит число N – количество чисел в наборе. Во второй строке теста содержится N чисел, разделенных пробелом. Все числа во входных данных целые, принимающие значения от 2 до 1024.
 
Выходные данные 
В ответе выведите число с максимальным количеством простых делителей. Если таких чисел несколько, выведите наименьшее из них.
 
Примеры
№ Входные данные Выходные данные
1
10
3 5 7 9 11 13 15 17 19 21
 15
2
11
2 4 6 8 10 13 39 105 200 201 143
 105

ID 38238. 2011
Темы: Целые числа    Простые числа и разложение на множители   

Представьте число 2011 в виду суммы K последовательных простых чисел (то есть простых чисел, между которыми нет других простых чисел). Например, число 31 можно представить в виде суммы трех посдедовательных простых чисел следующим образом: 7 + 11 + 13 = 31.

Входные данные
Вводится одно натуральное число K (от 1 до 2011).

Выходные данные
Выведите слагаемые в порядке возрастания, разделяя их пробелом.

Если разложить в сумму K слагаемых невозможно, выведите NO SOLUTION (заглавными буквами).

Примеры
№ Входные данные Выходные данные
1 3 661 673 677
2 2 NO SOLUTION

ID 38356. Сломанный калькулятор
Темы: Простые числа и разложение на множители   

У калькулятора есть две ячейки памяти: содержимое первой из них всегда отображается на табло, вторая является буфером. В начальный момент времени на табло калькулятора отображается целое число X, а в буфере записано число 0. У калькулятора работают только две клавиши: «+» и «=». При нажатии на «+» число, которое в данный момент отображено на табло, копируется в буфер. При нажатии на «=» число из буфера прибавляется к числу, отображенному на табло и результат отображается на табло, число в буфере при этом не меняется.

Требуется за наименьшее число нажатий клавиш на калькуляторе добиться того, чтобы на табло было отображено число Y.

Входные данные
Входной файл содержит два целых числа X и Y. Каждое из этих чисел по модулю не превышает 109.

Выходные данные
В первую строку выходного файла выведите одно число — количество нажатий клавиш, которое потребуется для получения числа Y. Если из числа X получить число Y с помощью указанных операций невозможно, в выходной файл выведите одно число –1.

Примеры
№ Входные данные Выходные данные
1 -1 -8 6
2 2 16 6
3 0 0 0

ID 38433. Степень
Темы: Простые числа и разложение на множители   

Для того чтобы проверить, как ее ученики умеют считать, Мария Ивановна каждый год задает им на дом одну и ту же задачу — для заданного натурального A найти минимальное натуральное N такое, что N в степени N (N, умноженное на себя N раз) делится на A. От года к году и от ученика к ученику меняется только число A.
Вы решили помочь будущим поколениям. Для этого вам необходимо написать программу, решающую эту задачу.
Формат входных данных
Во входном файле содержится единственное число A (1 ≤ A ≤ 1000000000 — на всякий случай; вдруг Мария Ивановна задаст большое число, чтобы кого-нибудь “завалить”).
Формат выходных данных
В выходной файл выведите единственное число N.
 

Примеры
№ Входные данные Выходные данные
1 8 4
2 13 13

ID 38575. Псевдопростые числа
Темы: Простые числа и разложение на множители   

Пусть a1 = 2, a2 = 3, an = a1·a2·...·an-1 – 1 при n ≥ 3. Назовем числа ai псевдопростыми. Для заданного натурального числа X нужно ответить на вопрос: можно ли X однозначно представить в виде произведения псевдопростых чисел (представления, отличающиеся только порядком множителей, считаются одинаковыми), и, если можно — выдать разложение.<

Входные данные
Вводится одно натуральное число X, 1 < X ≤ 109.

Выходные данные
Выведите псевдопростые числа, произведение которых равно X, в произвольном порядке. Если разложения не существует или оно не единственно, выдать 0.
 

Примеры
№ Входные данные Выходные данные
1 6 2 3
2 5 5
3 7 0

ID 38731. Минимальный делитель
Темы: Простые числа и разложение на множители    Цикл while   

Найдите самый маленький натуральный делитель числа x, отличный от 1 (2 <= x <= 30000).

Входные данные
Вводится натуральное число x.

Выходные данные
Выведите наименьший делитель числа x, отличный от 1.

Примеры
№ Входные данные Выходные данные
1 6 2

ID 38732. Делители числа
Темы: Цикл for    Простые числа и разложение на множители    Условный оператор   

Выведите все натуральные делители числа x в порядке возрастания (включая 1 и само число).

Входные данные
Вводится натуральное число x

Выходные данные
Выведите все делители числа x

 

Примеры
№ Входные данные Выходные данные
1 32 1 2 4 8 16 32 

ID 38733. Количество делителей
Темы: Простые числа и разложение на множители    Цикл for   

Подсчитайте количество натуральных делителей числа x (включая 1 и само число; x2109).

Входные данные
Вводится натуральное число x.

Выходные данные
Выведите единственное число - количество делителей числа x.
 

Примеры
№ Входные данные Выходные данные
1 32 6

ID 44036. Уравновесить подарки
Темы: НОД и алгоритм Евклида    Простые числа и разложение на множители   

У Деда Мороза есть N мешков с подарками. Каждый мешок имеет вес a1, a2, ..., aN. Для равномерной нагрузки на сани Деду Морозу необходимо, чтобы вес всех мешков был одинаковым. Чтобы этого добиться, Дед Мороз своим волшебным посохом может выполнить одну из следующих операций любое количество раз, возможно ноль раз.

  • Дед Мороз может выбрать любой мешок и если его вес кратен двум, то уменьшить вес в два раза.
  • Дед Мороз может выбрать любой мешок и если его кратен трем, то уменьшить вес в три раза.

На каждую операцию у Деда Мороза уходит 1 секунда.

Найдите минимальное общее количество секунд, которое необходимо Деду Морозу, для достижения одинакового веса всех мешков с подарками. Если нет способа достичь цели, выведите вместо этого значение -1.



Входные данные
Программа получает на вход в первой строке целое число N (2 <= N <= 1000). Во второй строке записаны N чисел ai - вес i-го мешка с подарками (1 <= ai <= 109).


Выходные данные
Выведите ответ на задачу.
 
 
Примеры
№ Входные данные Выходные данные
1 3
1 4 3		 3
2 3
2 7 6		 -1
3 6
1 1 1 1 1 1 		 0

ID 21952. Выборы
Темы: Алгоритмы на графах    Простые числа и разложение на множители    Динамическое программирование    Динамическое программирование: один параметр   

Скоро в Соединенных Штатах Берляндии пройдут выборы президента. На эту ответственную должность претендуют два кандидата: Дядя Сэм и Дядя Фродо. Вы работаете аналитиком в пред- выборном штабе Дяди Сэма, и вам поручено помочь ему победить конкурента. Раздуть газетный скандал из одержимости оппонента бросанием колец в жерла вулканов не получилось, так что при- дётся воспользоваться математикой.

Казалось бы, чтобы выиграть, необходимо убедить проголосовать за нашего кандидата более половины пришедших на выборы. Оказывается, что иногда нужно гораздо меньше! Для того чтобы понять, как это возможно, рассмотрим подробнее процедуру голосования.

Как вы знаете, Соединенные Штаты Берляндии разделены на несколько административных ре- гионов первого уровня — штатов. Сначала в каждом из штатов проходят местные выборы, по итогам которых каждый штат отдаёт свой голос за одного из кандидатов. Если не менее половины штатов выбрало Дядю Сэма, то выигрывает он (в случае равенства голосов Дядя Сэм имеет преимущество как действующий президент), иначе побеждает Дядя Фродо. Все штаты, в свою очередь, состоят из административных регионов второго уровня, каждый из которых представлен выборщиком из административных регионов третьего уровня и так далее. Последний уровень состоит из отдельных жителей Берляндии. Всего в Берляндии N жителей и K уровней административных единиц. Одним из ключевых принципов этой страны является равенство, так что любой регион i-го уровня делится на одинаковое число регионов следущего уровня (в том числе содержит одинаковое число граждан).

Так получилось, что делением на регионы поручили заняться именно вам, то есть в ваших руках назначить, на сколько именно административных единиц i-го уровня делится (i−1)-ая администра- тивная единица.

Также у вас есть сильный инструмент влияния на выбор людей — нефтяные бурли. Чтобы заста- вить одного избирателя отдать свой голос за Дядю Сэма, достаточно дать ему скромный подарок в размере одного нефтяного бурля.

К несчастью, изначально все N жителей Соединённых Штатов Берляндии собираются отдать свой голос за Дядю Фродо. Требуется определить минимальное количество нефтяных бурлей, ко- торое достаточно потратить для победы на выборах.

Формат входных данных

В единственной строке ввода находятся два целых числа N и K (1 <= N <= 1015 , 1 <= K <= 10).

Формат выходных данных
Требуется вывести единственное число — минимальное количество нефтяных бурлей, которое придётся потратить на предвыборные подарки при наилучшем разбиении на регионы.

Примеры

Ввод Вывод
9 2 4
12 3 2

Замечание
Берляндские законы не запрещают, чтобы страна состояла из одного штата, а город — одного жителя. Аналогично с остальными типами регионов.

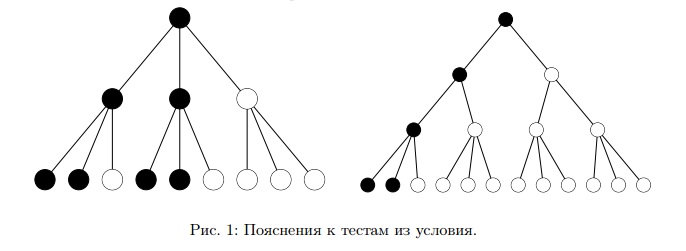
На рисунке 1 черным цветом отмечены те регионы, в которых победил Дядя Сэм. На нижнем уровне черными изображены вершины, соответствущие подкупленным конкретным жителям.