| Условие задачи | | Прогресс |
|
Темы:
Бинарный поиск
Сканирующая прямая
В зале ожидания на вокзале стоят N рядов из M кресел. Чтобы ожидающие не скучали, вместо некоторых кресел установлено K мощных Wi-Fi роутеров. Ожидающие стараются занять места ближе к роутерам, так как тогда они смогут смотреть ролики с Youtube или VK с более высоким разрешением, без задержек. Если пассажир сидит на месте с номером c в ряде r, а i-й роутер расположен на месте Ci в ряде Ri, то расстояние до i-го роутера вычисляется как max(|r−Ri|,|c−Ci|), где |x| – абсолютное значение x. Креслам в зале ожидания был присвоен приоритет от 1 до N⋅M−K, меньшие номера получили кресла с меньшим расстоянием до ближайшего роутера, среди кресел с одинаковым расстоянием до роутеров более удобными считаются кресла, стоящие в ряду с меньшим номером, а среди них — с меньшим номером места в ряду. На рисунке показан приоритет кресел в зале ожидания с 4 рядами из 7 кресел, в котором установлены 2 роутера (их позиции помечены черным цветом). Темно-серым цветом выделены кресла, стоящие на расстоянии 1 от роутеров, светло-серым — на расстоянии 2, белым — 3.
Напишите программу, которая вычисляет расстояние до ближайшего роутера от кресла с некоторым заданным приоритетом.
Первая строка ввода содержит четыре целых чисел — количество рядов N (2 ≤ N ≤ 109) и мест в ряду M (2 ≤ M ≤ 109), количество роутеров K (1 ≤ K ≤ 100, K < N⋅M), количество запросов Q (1 ≤ Q ≤ 100). Далее следует K строк, содержащих два целых числа — местонахождение роутеров: номер ряда Ri (1 ≤ Ri ≤ N) и номер места в ряду Ci (1 ≤ Сi ≤ M). Среди них нет совпадающих. Далее следует строка, содержащая Q целых чисел в диапазоне от 1 до N⋅M−K – приоритеты кресел.
Вывести для каждого запроса на отдельной строке одно целое число — расстояние до ближайшего роутера от кресла с заданным приоритетом.
| Ввод |
Вывод |
|
4 7 2 4
2 5
4 4
1 6 16 26
|
1
1
2
3
|
| |
![]()
|
|
Темы:
Бинарный поиск
Бинарный поиск в массиве
Вася загадал число от 1 до N. За какое наименьшее количество вопросов (на которые Вася отвечает "да" или "нет") Петя может угадать Васино число?
Входные данные
Вводится одно число N
Выходные данные
Выведите наименьшее количество вопросов, которого гарантированно хватит Пете, чтобы угадать Васино число.
| |
![]()
|
|
Темы:
Бинарный поиск
Быстрая сортировка
В одной из компьютерных игр-квестов есть следующее задание. На карте игрового мира размещены N персонажей, с каждым из которых может встретиться игрок. От общения с i-м персонажем карма игрока меняется на величину ai, которая может быть как положительной, так отрицательной или даже нулем.
Изначально карма игрока равна нулю. Для того чтобы пройти на следующий уровень, нужно чтобы карма была в точности равна значению K, при этом карма также может принимать как положительные, так и отрицательные значения.
Комнаты, в которых находятся персонажи, соединены односторонними магическими порталами, поэтому игроку придется встречать персонажей в определенной последовательности: после персонажа номер i он попадает к персонажу номер i + 1, затем к персонажу номер i + 2, и т.д. В комнате последнего персонажа с номером N портала к другому персонажу нет.
Для перемещения между персонажами можно использовать еще и заклинания телепортации, но к сожалению у героя осталось всего лишь два свитка с заклинаниями. Поэтому один из этих свитков придется использовать для того, чтобы телепортироваться к любому из персонажей, а второй свиток — чтобы покинуть игровой мир, после того, как карма героя станет равна K.
Помогите игроку определить, в какую комнату надо телепортироваться в начале и из какой комнаты нужно покинуть игровой мир, чтобы достичь кармы K или сообщите, что это невозможно.
Входные данные
В первой строке входных данных записаны два числа: количество персонажей N и необходимый уровень кармы K (|K| ≤ 109, K ≠ 0). Во второй строке через пробел записаны N целых чисел a1, a2, ..., aN — величины, на которые меняется карма героя после общения с персонажами с номерами 1, 2, ..., N соответственно.
Выходные данные
Выведите номер комнаты, в которую надо войти игроку и номер комнаты, из которой надо выйти, чтобы набрать карму K. Если возможных вариантов несколько, то необходимо вывести самый короткий путь, а если и таких несколько, то путь, начинающийся в комнате с как можно большим номером. Если достичь кармы K последовательно общаясь с персонажами невозможно, то выведите одно число - 1.
| Ввод |
Вывод |
5 3
-2 2 -1 2 4 |
2 4 |
7 1
1 -1 1 -1 1 -1 2 |
5 5 |
4 3
2 2 2 2 |
-1 |
| |
![]()
|
|
Темы:
Бинарный поиск
Напишите программу, которая находит в массиве элемент, самый близкий по величине к данному числу.
Формат входных данных
В первой строке задается одно натуральное число N, не превосходящее 1000 – размер массива. Во второй строке содержатся N чисел – элементы массива (целые числа, не превосходящие по модулю 1000). В третьей строке вводится одно целое число x, не превосходящее по модулю 1000.
Формат выходных данных
Вывести значение элемента массива, ближайшее к x. Если таких чисел несколько, выведите любое из них.
| |
![]()
|
|
Темы:
Бинарный поиск
Бинарный поиск в массиве
Реализуйте алгоритм приближенного бинарного поиска.
Формат входных данных
В первой строке входных данных содержатся числа N и K (\(0< N,\ K <100001\)). Во второй строке задаются N чисел первого массива, отсортированного по неубыванию. В третьей строке вводится K чисел второго массива.
Каждое число в обоих массивах по модулю не превосходит \(2 \cdot 10^9\).
Формат выходных данных
Для каждого из K чисел выведите в отдельную строку число из первого массива, наиболее близкое к данному. Если таких несколько, выведите меньшее из них.
| |
![]()
|
|
Темы:
Бинарный поиск
Бинарный поиск по ответу
В многопользовательской игре Agar.io игроки управляют бактериями. У каждой бактерии есть размер — целое положительное число. Если встречаются две бактерии разного размера, то бактерия большего размера поглощает меньшую бактерию. При этом меньшая бактерия исчезает, а размер большей бактерии увеличивается на размер меньшей бактерии. Если встречаются две бактерии равного размера, то ничего не происходит. Побеждает игрок, чья бактерия останется на игровом
поле одна.
В игре участвуют n игроков, вам даны размеры их бактерий. Определите, какие из игроков имеют возможность выиграть в этой игре.
Формат входных данных
Программа получает на вход целое число n, 1 ≤ n ≤ 105 — количество игроков. Следующие n строк содержат по одному числу ai — размеры бактерий, 1 ≤ ai ≤ 109. Числа ai заданы в порядке неубывания.
Формат выходных данных
Программа должна вывести n чисел равных «0» или «1», по одному числу в строке. Если i-е число равно 0, то это означает, что i-й игрок (размер бактерии которого первоначально был равен
ai) ни при каких обстоятельствах не может выиграть в этой игре. Если i-е число равно 1, то это означает, что i-й игрок имеет возможность выиграть в этой игре.
Примеры
| № |
Входные данные |
Выходные данные |
Пояснение |
| 1 |
4
1
1
3
4 |
0
0
1
1 |
В примере из условия 4 бактерии размерами 1, 1, 3, 4. Бактерии размером 1 никого не могут
съесть, поэтому не могут выиграть. Бактерия размером 4 может съесть всех. Бактерия размером 3
может съесть по очереди две бактерии размером 1. Тогда её размер станет 5, после этого она сможет
съесть бактерию размером 4 и выиграть. Ответ: 0, 0, 1, 1. |
| |
![]()
|
|
Темы:
Бинарный поиск
Префиксные суммы(минимумы, ...)
Цикл лекций в университете Флатландии посвящен изучению последовательностей.
Профессор называет последовательность целых чисел \(a_1, a_2, ..., a_n\) гармоничной, если каждое число, кроме \(a_1\) и \(a_n\), равно сумме соседних: \(a_2 = a_1 + a_3, a_3=a_2+a_4, ..., a_{n-1}=a_{n-2}+a_n\). Например, последовательность [1,2,1,–1] является гармоничной, поскольку 2=1+1, и 1=2+(–1) .
Рассмотрим последовательности равной длины: \(A=[a_1,a_2, ... a_n]\) и \(B=[b_1,b_2, ... b_n]\). Расстоянием между этими последовательностями будем называть величину \(d(A,B)= |a_1-b_1|+|a_2-b_2|+...+|a_n-b_n|\) . Например, \(d([1,2,1,–1][1,2,0,0])=|1–1|+|2–2|++|1–0|+|–1–0|=0+0+1+1=2 \)
В конце лекции профессор написал на доске последовательность из n целых чисел \(B=[b_1,b_2, ... b_n]\)и попросил студентов в качестве домашнего задания найти гармоничную последовательность \(A=[a_1,a_2, ... a_n]\), такую, что \(d(A, B)\) минимально. Чтобы облегчить себе проверку, профессор просит написать в качестве ответа только искомое минимальное расстояние \(d(A,B)\) .
Требуется написать программу, которая по заданной последовательности B определяет, на каком минимальном расстоянии от последовательности B найдется гармоничная последовательность A.
Входные данные
Первая строка входного файла содержит целое число n – количество элементов в последовательности ( \(3 \le n \le 300 000\)).
Вторая строка содержит n целых чисел \(b_1, b_2, …, b_n (–10^9 \le b_i \le 10^9 )\) .
Выходные данные
Выходной файл должна содержать одно целое число: минимальное возможное расстояние от последовательности во входном файле до гармоничной последовательности.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
1 2 0 0 |
2 |
| |
![]()
|
|
Темы:
"Два указателя"
Бинарный поиск
Задача на реализацию
Томми очень любит читать. Он взял из библиотеки n книг (в i-й книге ai страниц, страницы нумеруются с 1). Томми очень бережно относится к книгам, поэтому каждую из них обернул в обложку. Но, так как у него не оказалось ни одной прозрачной обложки, он пронумеровал книжки от 1 до n и написал номер на обложке каждой книги.
Томми читает уже m дней подряд. Книги он читает строго по порядку, начиная с книги с номером 1. Каждый день он записывает на доску общее число страниц, которые прочитал к текущему дню.
Например, если бы Томми взял 2 книги и, при этом, в в первой книге 3 страницы, а во второй - 5 страниц, то прочитав в первый день 2 страницы, а во второй день - 4 страницы у Томми на доске было бы записано два числа 2 и 6.
Томми сделал небольшой перерыв, а когда вернулся к чтению понял, что забыл какую книгу читал и на какой странице остановился. Также он не хочет терять статистику, но желает исправить ее, дописав в какой день какую книгу он читал и на какой странице остановился. Помогите Томми, по записанным числам на доске, определить в какой день какую книгу он читал и на какой странице остановился.
Входные данные
Программа получает на вход несколько строк. Первая строка содержит два целых числа n и m (1 <= n, n <= 2·105) - количество книг, взятых Томми из библиотеки и количество дней, в течении которых Томми читал книги. Во второй строке следует последовательность a1, a2, ... an (1 <= a1<= 1010), где ai равно количеству страниц в i-й книге. В третьей строке следует последовательность d1, d2, ... dm (1 <= dj <= a1 + a2 +...+ an), где dj равно общему числу страниц, прочитанных Томми к j-му дню. Все dj заданы в порядке возрастания.
Выходные данные
Выведите m строк. В каждой строке выведите по два числа - номер книги k (1 <= k <= n) и номер страницы в этой книге s (1 <= s <= ak), на которой остановился Томми в текущий день.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 6
10 15 12
1 9 12 13 15 17 |
1 1
1 9
2 2
2 3
2 5
2 7 |
| 2 |
2 3
5 10000000000
5 6 9999999999 |
1 5
2 1
2 9999999994 |
| |
![]()
|
|
Темы:
Деревья
Деревья
Структуры данных
Разреженные таблицы (sparse table)
Бинарный поиск
Префиксные суммы(минимумы, ...)
Колобку снится странный сон.
В нём Колобок находится на клетчатом поле размера n × m в клетке с координатами (x, y).
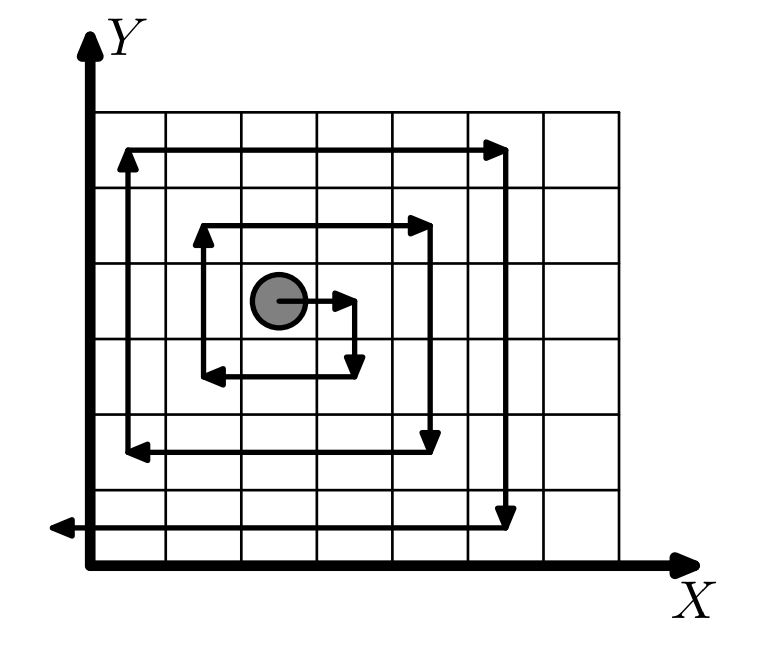
Изначально Колобок смотрит вдоль положительного направления оси X. Затем он начинает идти по полю со следующей закономерностью:
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на одну клетку вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на две клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на три клетки вперед. Повернуть на 90o вправо.
• Пройти на четыре клетки вперед. Повернуть на 90o вправо.
• И так далее...
Движение продолжается до тех пор, пока Колобок не выйдет за границы поля. После этого Колобок просыпается.
Утром Колобок решил проанализировать свой сон. Он догадался, что в каждой клетке он был максимум один раз, но никак не может вспомнить, сколько клеток он посетил. Колобок просит вас написать программу, которая посчитает количество посещённых им клеток.
Формат входного файла
В первой строке входного файла находятся два натуральных числа n, m (1 ≤ n, m ≤ 109 ) — размеры доски вдоль оси X и оси Y соответственно. Во второй строке находятся два натуральных числа x, y (1 ≤ x ≤ n; 1 ≤ y ≤ m) — координаты стартовой позиции колобка.
Формат выходного файла
В выходной файл выведите одно число — количество клеток, посещенных Колобком во сне.
| Вывод |
Ввод |
7 6
3 4 |
36 |
2 2
1 1 |
2 |
2 2
1 2 |
4 |
Комментарий
На рисунке наглядно показан первый пример.
| |
![]()
|
|
Темы:
Бинарный поиск по ответу
Бинарный поиск
Вы управляете армией штурмовиков, сражающейся против армии повстанцев. Армия повстанцев состоит из n солдат, здоровье i-го солдата составляет ai единиц. Сила атаки каждого вражеского солдата равна de единиц. В Вашем распоряжении есть m штурмовиков. Сила атаки каждого из них — dt , здоровье — h единиц.
Бой происходит в пошаговом режиме, пока с обеих сторон есть живые солдаты. Каждый шаг боя представляет собой одновременный выстрел всех живых солдат с обеих сторон. Каждый солдат может атаковать любого противника, но только одного. Несколько солдат с одной стороны могут атаковать одного и того же вражеского солдата. Здоровье солдата уменьшается на суммарную силу атаки солдат, атакующих его в течение этого хода. Если здоровье солдата в конце хода стало меньше или равно нулю, он погибает.
Ваша задача — уничтожить армию неприятеля, задействовав минимальное число штурмовиков, вне зависимости от действий противника, либо определить, что уничтожить вражескую армию не получится.
Формат входных данных
В первой строке входного файла заданы натуральные числа n, m, ( n,m <= 2*105), de, dt , h — число солдат в армии противника, число штурмовиков в вашем распоряжении, сила атаки каждого солдата неприятеля, сила атаки и число единиц здоровья каждого из штурмовиков соответственно ( de, dt , h <= 109). В следующей строке задано n натуральных чисел ai — число единиц здоровья i-го солдата армии противника (ai <= 109).
Формат выходных данных
Выведите единственное число — минимальное количество штурмовиков, необходимое для уни чтожения армии противника, либо -1, если миссия невыполнима.
| Ввод |
Вывод |
3 3 1 1 2
1 2 3 |
3 |
4 10 2 1 2
1 2 1 2 |
5 |
3 1 1 2 5
1 2 3 |
-1 |
| |
![]()
|
|
Темы:
Бинарный поиск
Целые числа
Вывод формулы
В лицее на уроках информатики ответы учеников оцениваются целым числом баллов от 2 до 5. Итоговая оценка по информатике выставляется как среднее арифметическое оценок на всех уроках, округленное до ближайшего целого числа. Если среднее значение находится ровно посередине между двумя целыми числами, то оценка округляется вверх.
Примеры округления оценок приведены в таблице.
| Оценки на уроках |
Среднее арифметическое |
Итоговая оценка |
| 2, 3, 5 |
\({ {2 + 3 + 5} \over 3 }= 3 {1 \over 3}\) |
3 |
| 3, 3, 4, 4 |
\({ {3 + 3 + 4 + 4} \over 4 }= 3 {1 \over 2}\) |
4 |
| 5, 5, 5, 3, 5 |
\({ {5 + 5 + 5 + 3 + 5} \over 5 }= 4 {3 \over 5}\) |
5 |
Все ученики лицея стремятся получить итоговую оценку по информатике не ниже 4 баллов. К сожалению, один из учеников получил на уроках a двоек, b троек и c четверок.Теперь он планирует получить несколько пятерок, причем хочет, чтобы итоговая оценка была не меньше 4 баллов. Ему надо понять, какое минимальное количество пятерок ему необходимо получить, чтобы добиться своей цели.
Требуется написать программу, которая по заданным целым неотрицательные числам a, b и c определяет минимальное количество пятерок, которое необходимо получить ученику, чтобы его итоговая оценка по информатике была не меньше 4 баллов.
Входные данные
Входные данные содержат три строки. Первая строка содержит целое неотрицательное число a, вторая строка содержит целое неотрицательное число b, третья строка содержит целое неотрицательное число c (0 ≤ a, b, c ≤ 1015, a + b + c ≥ 1).
Выходные данные
Выходные данные должны содержать одно число: минимальное число пятерок, которое необходимо получить ученику, чтобы итоговая оценка была не меньше 4 баллов.
| |
![]()
|
|
Темы:
Бинарный поиск
"Два указателя"
Вывод формулы
Группа юных археологов работает на раскопках здания древней библиотеки. Летом
они обнаружили остатки старой книги и, изучив их, сделали следующие выводы.
Книга содержит несколько страниц, каждая страница содержит либо текст, либо
иллюстрацию. Первые k страниц книги точно содержат иллюстрации. Все страницы книги
пронумерованы, но номер страницы написан только на страницах, содержащих текст. Сумма
номеров страниц с текстом равна s.
К сожалению, ни общее количество страниц в книге, ни количество иллюстраций
установить не удалось. Тем не менее, юных археологов заинтересовал вопрос, какое
минимальное количество иллюстраций могло быть в книге.
Например, если k = 1, а s = 8, то страницы книги могли иметь следующее содержание
(буквой «Т» обозначена страница, содержащая текст, а буквой «И» — страница, содержащая
иллюстрацию):
- И Т И И И Т, пронумерованы страницы 2 и 6, 4 иллюстрации;
- И И Т И Т, пронумерованы страницы 3 и 5, 3 иллюстрации;
- И И И И И И И Т, пронумерована страница 8, 7 иллюстраций.
Минимальное количество иллюстраций равно 3.
Требуется написать программу, которая по заданным целым числам k и s определяет
минимальное количество иллюстраций, которое могло быть в книге.
Формат входных данных
Первая строка входных данных содержит целое число k (0 ≤ k ≤ 109).
Вторая строка входных данных содержит целое число s (k + 1 ≤ s ≤ 1012).
Формат выходных данных
Требуется вывести одно целое число — минимальное количество иллюстраций в
| |
![]()
|
|
Темы:
Бинарный поиск
Задача на реализацию
Квартира Максима еще не прошла реновацию, поэтому температура в ней сильно зависит от температуры на улице. Для поддержания комфортной температуры он купил обогреватель и установил систему <<Умный дом>>. В соответствующую программу Максим заложил два целых числа \(t_{min} \leq t_{max}\) и следующий алгоритм использования обогревателя:
-
Если в течение последних пяти дней до текущего дня включительно обогреватель каждый день был выключен, и в каждый из этих дней температура на улице была строго меньше \(t_{min}\), то надо включить обогреватель в этот день и считать, что он был включен весь день. Обогреватель остается включенным и в последующие дни до тех пор, пока программа его не выключит.
-
Если в течение последних пяти дней до текущего дня включительно обогреватель каждый день был включен, и в каждый из этих дней температура на улице была строго больше \(t_{max}\), то надо выключить обогреватель в этот день и считать, что он был выключен весь день. Обогреватель остается выключенным и в последующие дни до тех пор, пока программа его не включит.
Из-за кратковременного отключения электроэнергии программу необходимо настроить заново. Сами значения \(t_{min}\) и \(t_{max}\) Максим забыл, зато у него остались записи программы о температуре и состоянии обогревателя в каждые из \(n\) дней использования системы.
Максим помнит, что \(t_{min}\) и \(t_{max}\) были целыми числами, по модулю не превосходящими \(10^9\) и \(t_{min} \leq t_{max}\), также он помнит, что программа не учитывала дни до первого дня использования системы и не включала обогреватель в течение первых четырех дней. Наконец, Максим помнит, что он выбирал \(t_{min}\) и \(t_{max}\) как можно более близкими друг к другу.
Помогите найти два подходящих значения \(t_{min}\) и \(t_{max}\), не превосходящих \(10^9\) по абсолютной величине, таких, что выполняются правила использования обогревателя в каждые из \(n\) дней, \(t_{min}\) не превосходит \(t_{max}\) и величина \(t_{max} - t_{min}\) минимальна.
Гарантируется, что записи программы правильные, и такие два числа существуют.
Формат входных данных
В первой строке задано целое число \(n\) (\(5 \leq n \leq 10^5\)) — количество дней, в течение которых работала система.
Во второй строке входных данных задаются \(n\) целых чисел \(t_1, \dots, t_n\) (\(-10^9 \leq t_i \leq 10^9\)) — температуры на улице в каждый из \(n\) дней.
В третьей строке входных данных задается строка из \(n\) символов, состоящая из 0 и 1 — если в \(i\)-й позиции данной строки записан 0, то это значит, что в \(i\)-й день обогреватель был выключен, а если 1, — то включен.
Формат выходных данных
В единственной строке выведите два целых числа \(t_{min}\) и \(t_{max}\) (\(t_{min} \leq t_{max}\)), по модулю не превосходящих \(10^9\) — значения температур, при вставке которых в программу обогреватель будет включен и выключен в те же дни, в которые он был включен и выключен при исходных значениях, а значение \(t_{max} - t_{min}\) минимально.
Если подходящих пар значений несколько, выведите любую из них.
Примечание
В первом тестовом примере первые пять дней температура строго меньше \(7\) градусов, при этом до пятого дня обогреватель был в каждый из четырех дней выключен, следовательно в пятый день программа его включила. На данный тест корректен любой ответ удовлетворяющий условию \(6 \leq t_{min} = t_{max} \leq 10^9\).
| |
![]()
|
|
Темы:
Бинарный поиск
На день рождения Пете подарили коробку кубиков. На каждом кубике написано некоторое целое число. Петя выложил все n своих кубиков в ряд, так что числа на кубиках оказались расположены в некотором порядке a[1], a[2],...,a[n]. Теперь он хочет раскрасить кубики в разные цвета таким образом, чтобы для каждого цвета последовательность чисел на кубиках этого цвета была строго возрастающей. То есть, если кубики с номерами i[1], i[2],..., i[k] покрашены в один цвет, то a[i[1]] < a[i[2]] < ... < a[i[k]]. Петя хочет использовать как можно меньше цветов. Помогите ему!
Входные данные
Первая строка входного файла содержит число n - количество кубиков у Пети (1 <= n <= 250000). Затем следует n чисел, разделенных пробелами и/или переводами строки - a[1], a[2], ..., a[n].
Выходные данные
На первой строке выходного файла выведите число L - наименьшее количество цветов, которое потребуется Пете. На следующей строке выведите n чисел из диапазона от 1 до L - цвета, в которые Петя должен покрасить кубики.
| |
![]()
|
Темы:
Бинарный поиск
Бинарный поиск по ответу
Быстрая сортировка
В одной демократической стране приближаются парламентские выборы. Выборы проходят по следующей схеме: каждый житель страны, достигший восемнадцатилетнего возраста, отдает свой голос за одну из политических партий. После этого партия, которая набрала максимальное количество голосов, считается победившей на выборах и формирует правительство. Если несколько партий набрали одинаковое максимальное количество голосов, то они должны сформировать коалиционное правительство, что обычно приводит к длительным переговорам.
Один бизнесмен решил выгодно вложить свои средства, и собрался поддержать на выборах некоторые партии. В результате поддержки он планирует добиться победы одной из этих партий, которая затем сформирует правительство, которое будет действовать в его интересах. При этом возможность формирования коалиционного правительства его не устраивает, поэтому он планирует добиться строгой победы одной из партий.
Чтобы повлиять на исход выборов, бизнесмен собирается выделить деньги на агитационную работу среди жителей страны. Исследование рынка показало, что для того чтобы один житель сменил свои политические воззрения, требуется потратить одну условную единицу. Кроме того, чтобы \(i\)-я партия в случае победы сформировала правительство, которое будет действовать в интересах бизнесмена, необходимо дать лидеру этой партии взятку в размере \(p_i\) условных единиц. При этом некоторые партии оказались идеологически устойчивыми и не согласны на сотрудничество с бизнесменом ни за какие деньги.
По результатам последних опросов известно, сколько граждан планируют проголосовать за каждую партию перед началом агитационной компании. Помогите бизнесмену выбрать, какую партию следует подкупить, и какое количество граждан придется убедить сменить свои политические воззрения, чтобы выбранная партия победила, учитывая, что бизнесмен хочет потратить на всю операцию минимальное количество денег.
Формат входных данных
Первая строка содержит целое число \(n\) — количество партий (\(1 \le n \le 10^5\)). Следующие \(n\) строк описывают партии. Каждая из этих строк содержит по два целых числа: \(v_i\) — количество жителей, которые собираются проголосовать за эту партию перед началом агитационной компании, и \(p_i\) — взятка, которую необходимо дать лидеру партии для того, чтобы сформированное ей в случае победы правительство действовало в интересах бизнесмена (\(1 \le v_i \le 10^6\), \(1 \le p_i \le 10^6\) или \(p_i = -1\)). Если партия является идеологически устойчивой, то \(p_i\) равно \(-1\). Гарантируется, что хотя бы одно \(p_i\) не равно \(-1\).
Формат выходных данных
На первой строке выведите минимальную сумму, которую придется потратить бизнесмену. На второй строке выведите номер партии, лидеру которой следует дать взятку. На третьей строке выведите \(n\) целых чисел — количество голосов, которые будут отданы за каждую из партий после осуществления операции. Если оптимальных решений несколько, выведите любое.
| |
![]()
|