Бор

Бор

Каждая вершина бора соответствует префиксу, некоторой добавленной строки. Сам это префикс получается путем последовательной записи символов на ребрах на пути от корня до этой вершины. При этом, каждому существующему префиксу соответствует ровно одна вершина. Корень бора соответствует пустой строке.

Пример бора для набора слов {be, bee, can, cat, cd}



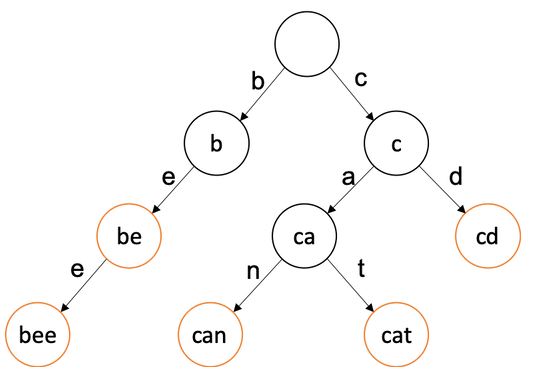
Оранжевым обозначены вершины, которые соответствуют самим словам из набора. Они называются терминальными.

Ниже представлен код хранения бора и добавления в него строк. Данный способ хранит бор через массив. Есть также реализация через указатели, которая представлена в коде задачи для тренировки.
 

// размер алфавита в рассматриваемых словах
const int alph = 26;

// структура для вершины бора
struct Node{
	// вектор ребер ввиде таблицы смежности, то есть:
	// next[0] - потомок при переходе по символу с номером 0 ('a')
	// next[1] - потомок при переходе по символу с номером 1 ('b')
	// и т.д.
	vector next;

	// дополнительные параметры
	// в данном случае высота вершины h и флаг терминальности
	int h;
	bool term;;

	Node(int h) {
		next.resize(alph, -1); // изначально без ребер
		this->h = h; // высота равно указанной
		term = false; // по умолчанию вершина не является терминальной
	}
};

// список вершин, изначально корень на нулевой высоте
vector trie(1, Node(0));

// функция добавления строки в бор
void add(const string& s) {
	int v = 0; // номер текущей вершины, начинаем из корня
	forn(i, (int)s.size()) {
		int c = s[i] - 'a'; // получаем номер текущего символа в строке

		// если нужного перехода еще нет, то сделаем новый
		if (trie[v].next[c] == -1) { 
			trie[v].next[c] = (int)trie.size(); // номер новой вершины равен 
                                                // текущему размеру бора (при 0-нумерации)
			trie.push_back(Node(trie[v].h + 1)); // создаем новую вершину с высотой на 1 больше
		}
		v = trie[v].next[c]; // переходим вдоль нужного ребра
	}

	// когда оказались в вершине, 
    // которая соответствует целой строке, 
    // то помечаем ее как терминальную
	trie[v].term = true;
}

Если вам необходимо поддерживать удаление строк из бора, то, вероятно, это получится делать нечестно. То есть просто снять флаг терминальности (или, возможно, вместо флага нужно будет хранить переменную числа), а само дерево бора оставить без изменений.

Таким образом, вставка/поиск/нечестное удаление работают за линейное время от длины строки-запроса.

Сам бор, в худшем случае, будет занимать O(n|Σ|) памяти, где n - суммарная длина всех строк, а Σ - алфавит используемых строк.

Для решения этой задачи вам сильно поможет теория об анализе игр: https://e-maxx.ru/algo/games_on_graphs