Сортировка вставками
Сортировка вставками (Insertion sort) — алгоритм сортировки, в котором элементы входной последовательности просматриваются по одному, и каждый новый поступивший элемент размещается в подходящее место среди ранее упорядоченных элементов.
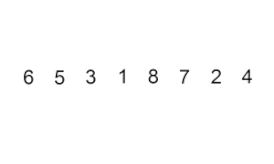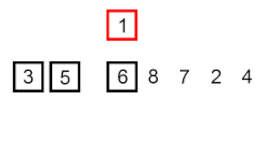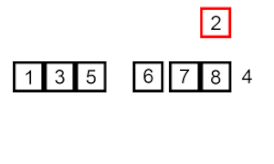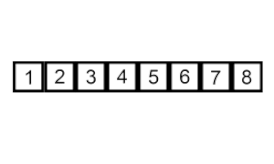
Сортировка вставками – это очень простой, но неэффективный алгоритм, который, тем не менее, имеет несколько конкретных преимуществ, которые делают его актуальным даже после того, как были разработаны многие другие, как правило, более эффективные алгоритмы.
При сортировке вставками вам не обязательно иметь весь массив заранее перед сортировкой. Алгоритм может получать по одному элементу в процессе сортировки. Это очень удобно, если нам нужно добавлять больше элементов во время сортировки. Алгоритм будет вставлять новый элемент в нужное место без «повторного выполнения» сортировки всего массива.
Сортировка вставками может использоваться на практике из-за ее эффективности для небольших (~ 10 элементов) наборов данных.
Задача заключается в следующем: есть часть массива, которая уже отсортирована, и требуется вставить остальные элементы массива в отсортированную часть, сохранив при этом упорядоченность. Для этого на каждом шаге алгоритма мы выбираем один из элементов входных данных и вставляем его на нужную позицию в уже отсортированной части массива, до тех пор пока весь набор входных данных не будет отсортирован. Метод выбора очередного элемента из исходного массива произволен, однако обычно (и с целью получения устойчивого алгоритма сортировки), элементы вставляются по порядку их появления во входном массиве.
Алгоритмическая реализация данного алгоритма
// Нулевой элемент считаем уже отсортированной последовательностью.
// Поэтому цикл начинаем с 1
ЦИКЛ ДЛЯ I=1 ДО N-1 ШАГ 1
X=A[I]
J=I
ПОКА J>0 AND A[J-1]>X //ищем место для вставки
ОБМЕН A[J],A[J-1]
J=J-1
КОНЕЦ ПОКА
A[J]=X
СЛЕДУЮЩЕЕ I
Вычислительная сложность:
\(\displaystyle O(n^{2})\).