Двоичное дерево поиска — это двоичное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):
• Оба поддерева — левое и правое — являются двоичными деревьями поиска.
• У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных самого узла X.
• У всех узлов правого поддерева произвольного узла X значения ключей данных больше либо равно (иногда строго больше, зависит от задачи), нежели значение ключа данных самого узла X.
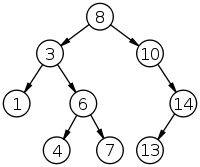
Проблема:
Казалось бы, что его структура позволяет выполнять различные операции (вставка, поиск, удаление) за O(logn), но это не так.
Двоичное дерево поиска может вытянуться в “бамбук”, тогда все операции будут выполняться за О(n). Вот пример подобного дерева:
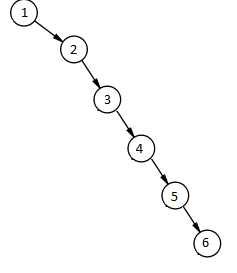
Решение:
В 1989 г. Сидель и Арагон решили эту проблему, предложив дерамиду (дерево + пирамида).
Дерамида хранит пары (X,Y) в виде бинарного дерева таким образом, что она является бинарным деревом поиска по x и бинарной пирамидой по y. Предполагая, что все X и все Y являются различными, получаем, что если некоторый элемент дерева содержит (X0,Y0), то у всех элементов в левом поддереве X < X0, у всех элементов в правом поддереве X > X0, а также и в левом, и в правом поддереве имеем: Y < Y0.
P.S. X и Y все-таки могут совпадать, ничего страшного в этом нет, хотя вероятность такой ситуации крайне мала.
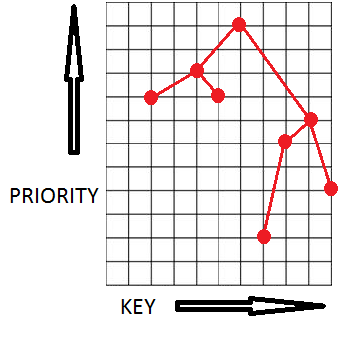
Декартово дерево
Декартово дерево – структура данных, основанная на дерамиде.
ДЕКАРТОВО ДЕРЕВО ПО ЯВНОМУ КЛЮЧУ
Для хранения декартового дерева создадим структуру Node (узел), которая будет являться вершиной дерамиды. Она будет хранить в себе ссылки (указатели) на левого и правого ребенка, Key(x), Priority(y).
В коде:
Struct Node {
Node* left_son;
Node* right_son;
Int key, priority;
};
Приоритет необходимо будет генерировать случайно:
#include <iostream>
#include <ctime>
#include <cstdlib>
using namespace std;
Int main()
{
srand(time(NULL));
int priority = rand();
return 0;
}
Создание нового узла:
Node* now = new Node {NULL, NULL, k, pr};
Наше дерево будет обладать двумя основными способностями:
1) Его можно будет разрезать на 2 дерева (split)
2) Два дерева можно будет соединить в одно (merge)
В результате этих операций мы будем получать корректные деревья.
Описание операций:
1) Split – будет разрезать одно дерево на два по ключу k. В результате в первом дереве будут находиться все вершины с ключами в диапазоне [min(key); k). Во втором же [k; max(key)].
Split – рекурсивная функция, возвращающая пару Node*(корни получившихся деревьев). В качестве параметра принимает корень дерева, которое мы режем, и ключ k, по которому мы режем.
Порядок действий:
Посмотрим на ключ текущей вершины. Логично, что если его ключ >= ключу, по которому мы режем, то мы должны резать левого сына (рекурсивный запуск). Вместо левого сына у нас будут 2 поддерева: левое, в котором будут находится вершины с нужными ключами и правое, в котором останутся все остальные. Чтобы в конечном итоге у нас осталось 2 корректных дерева, необходимо сделать правый остаток от разрезания левого сына левым ребенком дерева, которое мы изначально рассматривали. Далее можно будет вернуть получившиеся деревья.
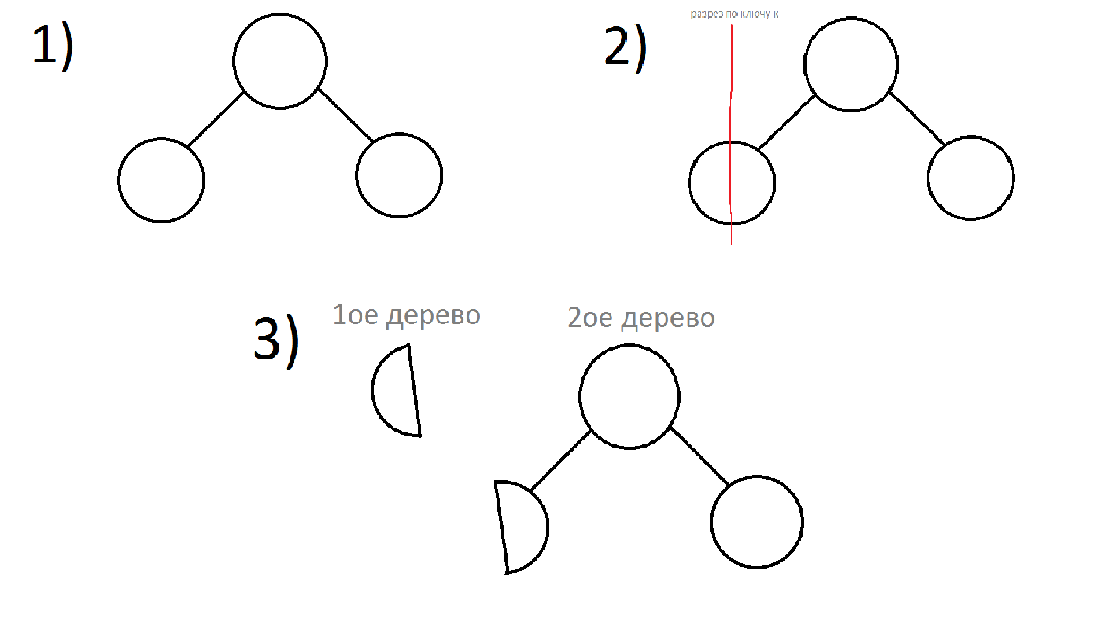
Если ключ текущего узла < чем ключ, по которому режем, то резать нужно правое поддерево. Вместо правого сына у нас будут 2 поддерева: правое, в котором будут находится вершины с нужными ключами и левое, в котором останутся все остальные. Чтобы в конечном итоге у нас осталось 2 корректных дерева, необходимо сделать левый остаток от разрезания правого сына правым ребенком дерева, которое мы изначально рассматривали. Далее можно будет вернуть получившиеся деревья.
P.S. Просто те же действия, что и с левым, только наоборот.
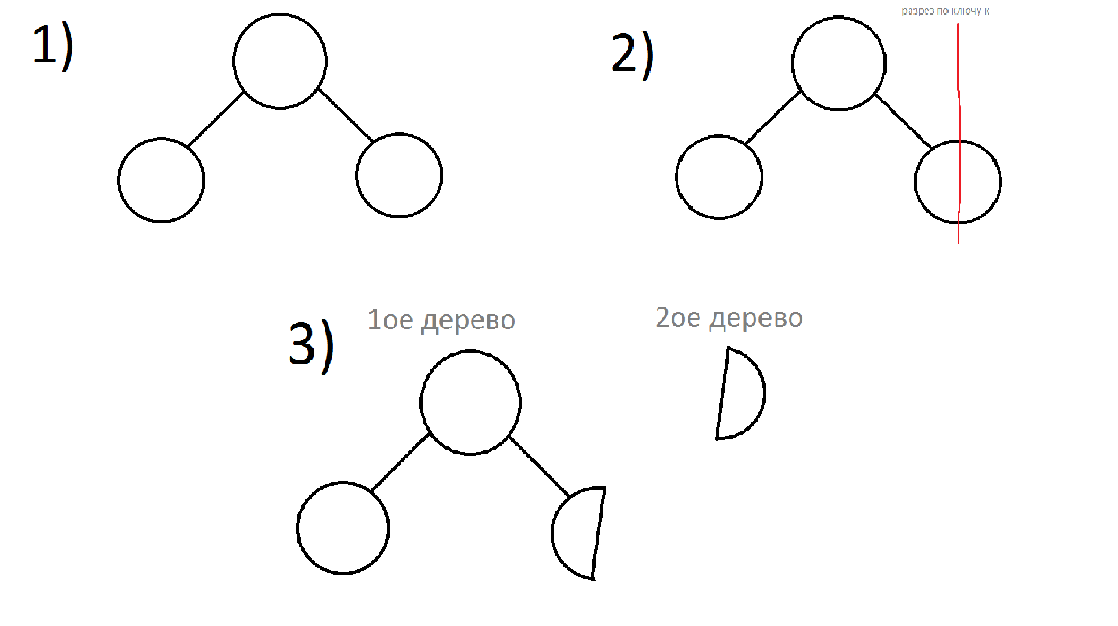
P.S. Если вершина, которую мы режем не существует ( у листов ссылки на сынов будут NULL), то надо будет вернуть 2 пустоты. (пустота + пустота = пустота).
2) Merge – будет соединять два дерева в одно, в зависимости от приоритетов деревьев.
Merge – рекурсивная функция, которая возвращает Node* (корень полученного дерева). В качестве параметров принимает 2 Node* (корни деревьев, которые мы соединяем).
Порядок действий:
Сравним приоритеты двух данных деревьев. Если приоритет левого больше, то соединим ( рекурсивный вызов) его правого ребенка с правым данным деревом.
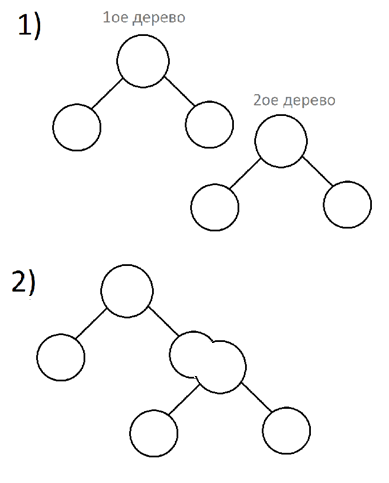
Если больше приоритет правого, то соединим (рекурсивный вызов) его левого ребенка с левым данным деревом.
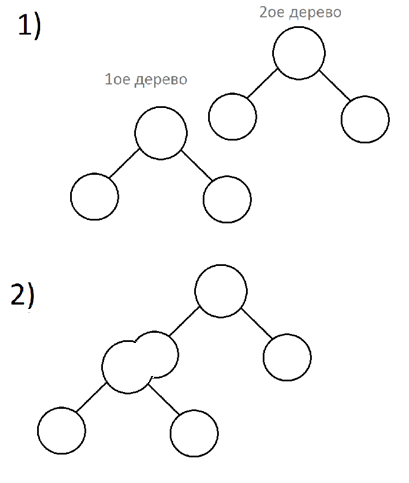
Важное замечание:
Заметим, что изначально корень дерева и все листы в уже непустом дереве не будут иметь детей ( т.е. будут иметь нулевые указатели(указатели на ничего) ).
Обращение к нулевому указателю приводит к ошибке исполнения, поэтому решить эту проблему можно множеством условных операторов или же созданием определенного узла, который будет являться фиктивной вершиной. И вместо нулевых указателей будем делать указатель на данные узлы. В таком случае ошибки исполнения не будет, но необходимо аккуратно использовать такие вершины.
Node* empty = new Node {NULL, NULL, 0, 0}; - Фиктивная вершина (пустота).
Тогда создание новой вершины будет иметь следующий вид:
Node* now = new Node {empty, empty, k, pr};
В операциях split и merge необходимо обрабатывать отдельно случаи, когда дерево является пустотой, а именно:
1) Если разрезать пустоту, будет две пустоты.
2) Если соединить что-то с пустотой, то это что-то не изменится.
Построение и изменения дерева:
Для изменения дерева нам понадобятся две функции:
1) Insert
Будет добавлять в дерево узел с ключом k.
Для этого по-split-им дерево по ключу k, создадим новый узел, по-merge-им левое дерево от разреза с новым узлом, а потом получившееся с правым от разреза деревом.
2) Erase
Будет удалять из дерева узел с ключом k.
Для начала по-split-им дерево по ключу k. Как мы помним, в первом дереве будут находиться все вершины с ключами в диапазоне [min(key); k), а во втором же [k; max(key)]. Далее по-split-им правое от разреза дерево по ключу k + 1. В итоге у нас будут 3 поддерева: с ключами менее k, с ключом k и ключами более k. С-merge-им поддеревья с ключами менее и более k, а про узел с ключом k просто забудем.
Построение дерева:
Изначально у нас будет узел “корень”, который будет представлять из себя “пустышку”. Далее просто будем insert-ить все необходимые узлы в дерево.
Поддержание параметра в декартовом дереве
Скорее всего вам захочется поддерживать какой-нибудь параметр ( сумма, минимум и т.п. по ключам) в данной структуре, ведь все запросы будут осуществляться за O(log n).
Создадим новое поле в структуре, которое будет отвечать за значение нужного параметра в поддереве. Значение параметра в определенном узле – это значение в поддереве, корнем которого является этот узел.
Для поддержания корректного значения параметра создадим процедуру update.
Update будет пересчитывать параметр через своих детей и себя.
Например:
v->sum = v->left_son->sum + v->right_son->sum + v->key;
v->min = min( min(v->left_son->min, v->right_son->min), v->key)
v->size = v->left_son->size + v->right_son->size + 1
Где v – текущий узел.
Update не должен обновлять фиктивные вершины.
Теперь перед каждым возвратом в split и merge будем обновлять то, что возвращаем. В итоге получим корректные значения.
Теперь чтобы узнать параметр в определенном поддереве, вы-split-им это поддерево и обратимся к полю, отвечающее за параметр. Там определенно будет корректное значение.
ДЕКАРТОВО ДЕРЕВО ПО НЕЯВНОМУ КЛЮЧУ
Декартово дерево по неявному ключу представляет собой немного измененное декартово дерево по явному ключу. Теперь каждая вершина будет характеризоваться не ключом, а порядковым номером. Таким образом, теперь дерево будет обладать следующим свойством: для каждой вершины выполняется, что все порядковые номера вершин в левом поддереве меньше, а в правом поддереве больше, чем ее собственный номер. Таким образом, можно просто забыть про структуру упорядоченности дерева, и оно фактически по своему использованию превращается из двоичного дерева поиска в обычный массив.
Реализация:
Хранить порядковые номера в явном виде неудобно, при этом их изменение будет занимать долгое время, поэтому воспользуемся следующим фактом: порядковый номер каждой вершины равен кол-ву вершин с меньшим номером, то есть просто размеру левого поддерева. Размеры поддеревьев мы уже умеем хранить.
Однако теперь меняется операция split, т.к. ключа больше нет.
А именно: теперь дерево можно резать только по размеру. Алгоритм действий остается прежним (см. выше), меняется только условие по которому мы определяем в какого из двух детей мы рекурсивно запустимся.
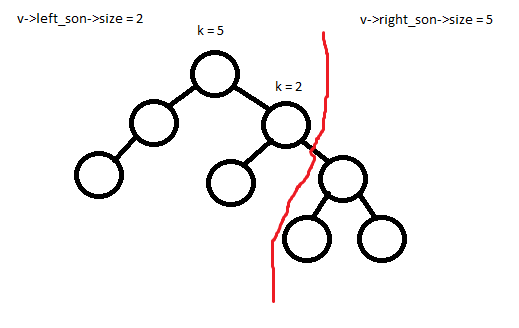
Пусть сейчас мы режем дерево v по размеру k (соответственно вернуться два дерева размера k и v->size – k). Теперь есть два очевидных случая:
1) Размер левого поддерева больше либо равен k. Тогда разрезать надо левого ребенка.
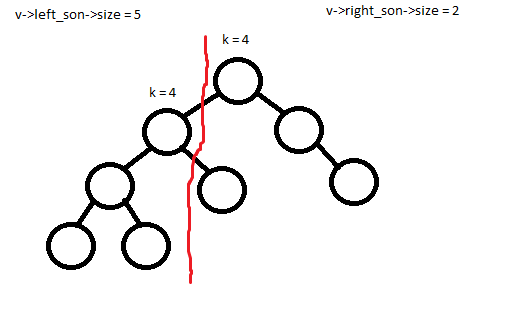
2)
Размер левого поддерева меньше, чем k. Тогда разрезать надо правого ребенка, но в таком случае все левое поддерево и данная вершина будут являться префиксом дерева размера k, которое вернется на текущем шаге, поэтому правого ребенка необходимо разрезать уже по размеру k – v->left_son->size – 1.
Операция merge никак не меняется.
Также немного изменяется (даже упрощается ) построение декартового дерева. Функции insert и erase больше не нужны, т.к. при добавлении вершин новую необходимо добавлять в самый конец дерева ( т.к. номер у нее самый большой). Фактически на каждом шаге это будет выглядеть как
root = merge(root, p);
где p – новая вершина (объявление см. выше).
Применения:
Теперь мы имеем мощную структуру данных которая умеет выполнять такие операции над массивом, как удаление и вставка подотрезков за время O(log(n)).
Например, необходимо перенести подотрезок [l;r] в конец массива. Для этого разрежем наше дерево на 3 следующими шагами:
1) Разрежем по l – 1
2) Правую часть от разрезания разрежем по r – l + 1
Получили L, M, R (left, mid, right) размеров l – 1, r – l + 1 и n – r соответственно. В дереве M будет как раз тот подмассив, который нам и нужен.
Далее просто скрепим их заново, но в другом порядке:
root = merge(merge(L, R), M);
Массовые операции:
Над декартовым деревом по неявному ключу возможно совершать массовые операции (прибавление на отрезке, изменение на отрезке и т.п.). Смысл тот же, что и для других структур данных: создадим в структуре Node новое поле, которое будет отвечать за ленивое изменение данного узла. Также создадим метод push, который будет совершать необходимый пересчет данного узла и передавать информацию детям. Метод push необходимо вызывать в самом начале операций split и merge.
Пример метода push, реализующий массовое прибавление. В дереве поддерживаются сумма в поддереве и значение в узле.
void push(Node* v)
{
if (v == empty)
return; // не обрабатываем фиктивные вершины
v->sum += (v->lazy * v->size);
v->value += v->lazy;
v->left_son->lazy += v->lazy; // пропихнули в левого ребенка
v->right_son->lazy += v->lazy; // пропихнули в правого ребенка
v->lazy = 0; // больше добавлять ничего не надо
}
Теперь чтобы выполнить массовую операцию на отрезке, достаточно вы-split-ить нужный подотрезок и изменить поле, отвечающее за ленивые операции у узла, который окажется корнем данного подотрезка. Далее обратно скрепить дерево в одно целое.
Чтобы узнать определенное значение на подмассиве необходимо также вырезать нужный подотрезок и спросить значение у нужного поля.
Гарантируется, что при правильной реализации это будет корректно работать.
Бонус
Декартово дерево умеет также делать разворот на отрезке! Каким образом это возможно? Вспомним свойство декартово дерева по неявному ключу - для каждой вершины выполняется, что все порядковые номера вершин в левом поддереве меньше, а в правом поддереве больше, чем ее собственный номер. Тогда при развороте должно быть ровно наоборот, следовательно достаточно лишь для каждого узла поменять местами его левого и правого ребенка ( swap(v->left_son, v->right_son) ). Опять же заведем поле lazy (ленивое изменение), которое будет говорить нужно ли поменять местами детей (буловый флажок). В push при истином значении флажка поменяем местами детей и сделаем его равным false. Однако необходимо быть аккуратным при передачи информации детям! Просто сказать, что lazy у них должно быть истиной будет неверно, т.к. оно до этого могло быть истиной, а это значит, что на данный момент мы должны развернуть то, что развернуто, а следовательно, просто оставить без изменений (развернув массив дважды вы получите исходный массив). Необходимо каждый раз менять значение lazy на противоположное.
void push(Node* v)
{
if (v == empty || v->lazy == false) // если не надо разворачивать, то сразу выйдем
return;
swap(v->left_son, v->right_son);
v->left_son->lazy ^= true;
v->right_son->lazy ^= true;
v->lazy = false;
}
(с) Курбатов Е., 2018