Задача: Архимедова спираль
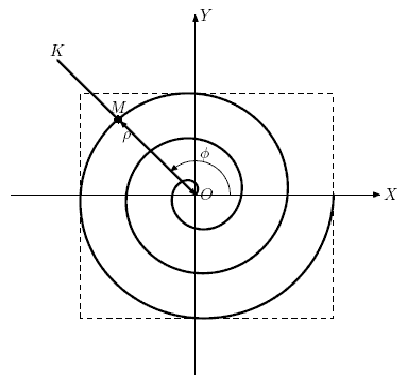
Дима недавно поступил на работу в НИИ Плоских Кривых. Как следует из названия этого научно- исследовательского института, он занимается различными исследованиями в области плоских кривых. Недавно Димин начальник Георгий столкнулся с весьма интересной кривой, которая, как выяснилось после некоторого исследования, известна под названием Архимедовой спирали. Архимедова спираль плоская кривая, изображающая траекторию точки M, которая равномерно движется вдоль луча OK с началом в O, в то время как сам луч OK равномерно вращается вокруг точки O (см. рисунок). Другими словами, расстояние до начала координат ρ = OM линейно зависит от угла поворота φ луча OK. При этом повороту луча OK на один и тот же угол соответствует одно и то же приращение расстояния ρ.
Движение точки M можно задать с помощью ряда параметров:
• начального угла поворота α луча OK (измеряется в градусах против часовой стрелки относительно положительного направления оси OX);
• угловой скорости вращения ω луча OK (измеряется в градусах за единицу времени);
• начального расстояния R от точки M до начала координат (точки O);
• скорости движения V точки M по лучу OK.
Если, задав эти параметры, не ограничить время движения точки M, то получится бесконечная кривая, исследовать которую достаточно трудно. Поэтому Дима решил ограничиться исследованием некоторой части этой кривой той, которая получается при движении точки M от нулевого момента времени до момента времени T. Задача, которую решает Дима состоит в поиске прямоугольника минимальной площади со сторонами, параллельными осям координат, в который ее можно вписать.
Требуется написать программу, которая найдет искомый прямоугольник
Входные данные
Входной файл содержит четыре целых числа: ω (1 ≤ ω ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) и T (1 ≤ T ≤ 1000). В этой задаче считается, что начальный угол поворота α равен нулю.
Выходные данные
В первой строке выходного файла выведите два вещественных числа — координаты левого нижнего угла искомого прямоугольника, а во второй строке — координаты правого верхнего угла искомого прямоугольника.
Ответ будет считаться правильным, если значение каждой из координат будет отличаться от истинного значения не более чем на 10-5.
Ваш ответ: