Задача: Соединение точек
«Соединение точек» – это игра для одного игрока. Игровое поле строится следующим образом. Выбираются два целых числа, каждое из которых больше 2, которые обозначаются g и r. Затем на плоскости рисуются четыре точки в вершинах квадрата, две верхние из них становятся зелеными точками, а две нижние – красными. Далее внутри квадрата рисуются зеленые и красные точки таким образом, что никакие три точки, включая вершины квадрата, не лежат на одной прямой. Процесс продолжается до тех пор, пока общее количество зеленых точек не станет равным g, а количество красных точек – равным r.
После того, как игровое поле нарисовано, игрок начинает соединять точки. Две точки можно соединять отрезком, соблюдая следующие условия:
*соединяются только две точки одного цвета;
*отрезок, соединяющий точки, не пересекает никакой из ранее нарисованных отрезков (кроме как по концам отрезков).
Будем считать, что две точки u и v принадлежат одной компоненте, если от u до v можно дойти по нарисованным отрезкам.
Цель игры – соединить все зеленые точки в одну компоненту с помощью (g – 1) отрезков, а все красные точки – в другую компоненту с помощью (r – 1) отрезков. Можно доказать, что при вышеописанном способе расположения точек всегда существует способ выиграть игру.
Вам будет задано квадратное игровое поле со стороной s, а также g зелеными и r красными точками. Координаты точек задаются парами целых чисел (xi, yi). Зеленые точки пронумерованы числами от 1 до g так, что верхняя левая точка (0, s) имеет номер 1, верхняя правая точка (s, s) – номер 2, а остальные точки – номера от 3 до g (в произвольном порядке). Красные точки пронумерованы числами от 1 до r так, что нижняя левая точка (0, 0) имеет номер 1, нижняя правая точка (s, 0) – номер 2, а остальные точки – номера от 3 до r (в произвольном порядке).
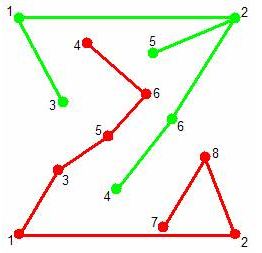
На рисунке показан пример игры, где зеленые точки соединены в одну компоненту, а красные точки – в другую.
Легко видеть, что никакие три точки на рисунке не лежат на одной прямой, и никакие два отрезка не пересекаются, кроме как по концам.
Задание
Напишите программу, которая по заданным координатам g зеленых точек и координатам r красных точек находит способ, как нарисовать (g – 1) зеленых отрезков и (r – 1) красных отрезков таким образом, чтобы все зеленые точки принадлежали одной компоненте, а все красные точки – другой, и никакие два отрезка не пересекались.
Ограничения
3≤g≤50000,g – количество зеленых точек
3≤r≤50000
0<s≤200000000,r – количество красных точек
Входные данные
На вход Вашей программы поступают данные в следующем формате:
СТРОКА 1: Содержит целое число g.
СЛЕДУЮЩИЕ g
СТРОК: Каждая строка содержит два целых числа – координаты xi и yi каждой из g зеленых точек, начиная с точки с номером 1 и заканчивая точкой с номером g. Эти два числа разделены пробелами.
СТРОКА g + 2: Содержит целое число r.
СЛЕДУЮЩИЕ r СТРОК: Каждая строка содержит два целых числа – координаты xi и yi каждой из r красных точек, начиная с точки с номером 1 и заканчивая точкой с номером r. Эти два числа разделены пробелами.
Выходные данные
Ваша программа должна вывести (g – 1) + (r – 1) строк, каждая из которых описывает один отрезок, соединяющий две точки.
Каждая строка должна содержать два целых числа и один символ, разделенные пробелом. Числа представляют собой номера точек, соединенных этим отрезком. Если точки зеленые, то последним символом в строке должен быть g, если точки красные, то последним символом в строке должен быть r.
Ни порядок, в котором выводятся отрезки, ни порядок точек в строке не имеют значения.
Замечание
Если существует несколько маршрутов товароперевозок, удовлетворяющих всем указанным требованиям, выведите любой из них.
Ваш ответ: