Задача: День рожденья
Сегодня день рождения Никиты. На празднование дня рождения приглашены n детей (включая самого Никиту). Все дети пронумерованы числами от 1 до n. Работники МакДональдса приготовили большой круглый стол и поставили вокруг него n стульев.
Как только дети приходят на день рождения, они рассаживаются за столом. Ребенок с номером 1 занимает одно из мест. Ребенок с номером 2 занимает место слева от ребенка с номером 1. Ребенок с номером 3 занимает следующее за ним место слева и так далее. Наконец, ребенок с номером n
займет оставшееся свободное место между детьми с номерами n – 1 и 1.
Работники МакДональдса хорошо знают, что некоторые из приглашенных детей ведут себя весьма шумно за столом, если сидят друг с другом. Поэтому работники ресторана собираются пересадить детей в некотором порядке. Этот порядок описывается перестановкой p1, p1,..., pn (p1, p2,..., pn — различные целые числа от 1 до n). То есть, ребенок p1 должен сидеть между pn и p2, ребенок pi (i = 2, 3, ... , n − 1) должен сидеть между pi-1 и pi+1; ребенок pn должен сидеть между pn-1 и p1.
К сожалению, все дети пришли и расселись так, как указано в первом абзаце. Поэтому для того, чтобы рассадить детей в нужном порядке, придется пересадить кого-то из детей на некоторое количество мест влево или вправо. Для каждого ребенка работникам ресторана необходимо решить, как он будет пересаживаться: они должны выбрать направление (влево или вправо) и расстояние (на сколько мест нужно переместиться). Затем, по заданному сигналу все дети должны одновременно встать и переместиться на места, определенные работниками МакДональдса.
Пересаживание детей вносит беспорядок в празднование дня рождения. Величина беспорядка пропорциональна максимальному из расстояний, на которые дети будут пересажены. Пересаживание детей можно организовать многими способами. Работники МакДональдса решили выбрать тот из них, при котором величина беспорядка будет минимальной, то есть тот способ, при котором максимальное из расстояний пересаживания будет минимальным. Помогите им найти такой способ.
Имейте в виду, что ребенок pi может сидеть как слева, так и справа от ребенка pn.
Задание
Ваша задача — написать программу, которая:
· читает из стандартного ввода количество детей и перестановку, определяющую желаемый порядок рассадки детей,
· вычисляет минимально возможную величину беспорядка,
· выводит результат в стандартный вывод.
Входные данные
В первой строке стандартного ввода содержится единственное целое число n (1 ≤ n ≤ 1 000 000). Во второй строке содержатся n целых чисел p1, p2,..., pn, разделенных одним пробелом. Числа p1, p2,..., pn образуют перестановку множества {1, 2, ... , n}, описывающую желаемый порядок рассадки детей. Кроме того, в 50% тестов число n не будет превышать 1 000.
Выходные данные
В первую и единственную строку стандартного вывода выведите единственное число — минимально возможное из максимальных расстояний, на которые придется пересесть детям.
Пояснения
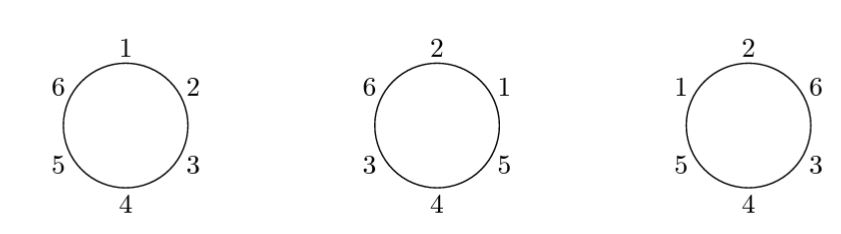
На рисунке слева изображена исходная рассадка детей. На рисунке в середине показан результат пересаживания, при котором дети с номерами 1 и 2 перемещаются на одно место, дети с номерами 3 и 5 перемещаются на два места и дети с номерами 4 и 6 не меняют своего положения. Требуемые условия рассадки выполнены, поскольку 3-й сидит между 6-м и 4-м, 4-й сидит между 3-м и 5-м, 5-й сидит между 4-м и 1-м, 1-й сидит между 5-м и 2-м, 2-й сидит между 1-м и 6-м и 6-й сидит между 2-м и 3-м. Также существует другой вариант конечной рассадки детей, изображенный на рисунке справа. В обоих вариантах величина беспорядка равна 2.
Ваш ответ: