Задача: Вышивка жемчугом
Со стародавних времён в поморских деревнях рукодельницы вышивали жемчугом на прямоугольных полотенцах, состоящих из одинаковых клеток. Вышивка начиналась с пришивания жемчужины к полотенцу в центре одной из клеток. Чтобы пришить новую жемчужину, рукодельница делала стежок из клетки, уже содержащей жемчужину, в соседнюю с ней по горизонтали или вертикали свободную клетку. Новая жемчужина пришивалась в центре клетки на конце стежка. Этот процесс повторялся, пока не заканчивались жемчужины.
Одно из таких праздничных полотенец находится в музее. К сожалению, некоторые части узора были утеряны, но описание полотенца сохранилось. Дирекция музея планирует восстановить один из прямоугольных фрагментов полотенца, но не ещё не решила какой именно. Затраты на восстановление фрагмента зависят от количества связных частей узора, попавших на этот фрагмент. Часть узора считается связной, если от любой её жемчужины можно по стежкам перейти к любой другой её жемчужине, не выходя за границы фрагмента. Дирекция всегда относит любые две жемчужины, между которыми можно перейти по стежкам, к одной и той же связной части узора.
Требуется написать программу, вычисляющую количество связных частей узора для каждого из заданных фрагментов.
Входные данные
Первая строка входных данных содержит два целых числа \(a\) и \(b\) — размеры полотенца в клетках по горизонтали и вертикали.
Вторая строка содержит два числа \(n\) и \(q\) — количество жемчужин в узоре и количество фрагментов соответственно.
Следующие \((n - 1)\) строк содержат описания стежков. Каждый стежок имеет один из следующих видов:
h \(x~y\) означает, что клетки с координатами \((x, y)\) и \((x + 1, y)\) содержат жемчужины, соединённые горизонтальным стежком (\(1 \leq x \leq a - 1\); \(1 \leq y \leq b\));v \(x~y\) означает, что клетки с координатами \((x, y)\) и \((x, y + 1)\) содержат жемчужины, соединённые вертикальным стежком (\(1 \leq x \leq a\); \(1 \leq y \leq b - 1\)).
Так как неизвестно в каком порядке рукодельница наносила стежки, их описания следуют в произвольном порядке. При этом гарантируется, что узор был получен в результате процесса, описанного в условии задачи.
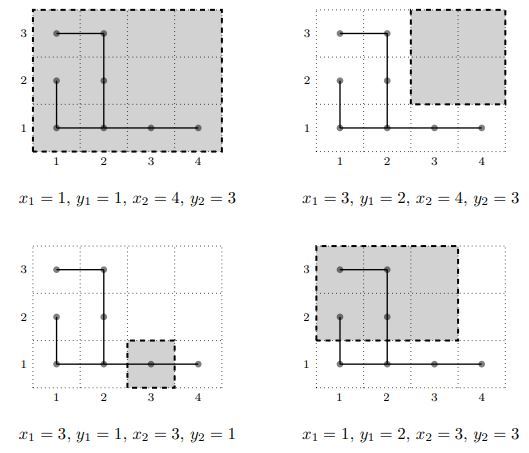
Следующие \(q\) строк описывают фрагменты. Каждое описание содержит четыре целых числа \(x_1\), \(y_1\), \(x_2\) и \(y_2\) — координаты левой нижней и правой верхней клетки фрагмента (\(1 \leq x_1 \leq x_2 \leq a\); \(1 \leq y_1 \leq y_2 \leq b\)).
Выходные данные
Выходные данные должны содержать \(q\) строк, где \(i\)-я строка содержит количество связных частей узора в \(i\)-м фрагменте.
Замечание
Пояснение к тесту из условия.
Ваш ответ: