Задача: Туристический маршрут
Школьники приехали на экскурсию в новый город и решили осмотреть его достопримечательности. Представим город в виде прямоугольной сетки \(n \times m\), в некоторых клетках которой могут находиться достопримечательности.
Друзья начинают свой путь в клетке \((1, 1)\), они хотят дойти до клетки \((n,m)\), а затем вернуться обратно. В городе есть \(k\) достопримечательностей, они расположены в клетках \((x_1, y_1), \ldots, (x_k, y_k)\), друзья обязательно хотят посетить их все.
За одну минуту можно перейти из клетки \((a, b)\) в клетку \((c, d)\), если они являются соседними по стороне, то есть выполняется равенство \(|a - c| + |b - d| = 1\). Легко видеть, что на маршрут необходимо потратить хотя бы \(2n+2m-4\) минут, будем рассматривать только такие маршруты.
Будем называть маршрут интересным, если выполняются следующие условия:
-
для того, чтобы пройти маршрут, друзья потратят ровно \(2n+2m-4\) минут;
-
маршрут проходит через каждую клетку не более одного раза.
-
маршрут проходит через все клетки, которые содержат достопримечательности.
Помогите школьникам понять, сколько существует различных интересных маршрутов. Так как это число может оказаться достаточно большим, то выведите его остаток при делении на \(10^9+7\).
В первой строке указаны числа \(n\), \(m\) и \(k\) (\(3 \le n,m \le 10^6\), \(0 \le k \le 2\,000\)).
В последующих \(k\) строках указано по паре чисел \(x_i\), \(y_i\) (\(1 \le x_i \le n\), \(1 \le y_i \le m\)), гарантируется, что все пары \((x_i, y_i)\) различны. То есть для любой пары индексов \((i, j)\) (\(1 \le i < j \le n\)) верно одно из двух: \(x_i \neq x_j\) или \(y_i \neq y_j\).
Выведите единственное число — остаток от деления числа интересных маршрутов на \(10^9+7\).
Примечание
Ниже изображены все интересные маршруты для первого теста.
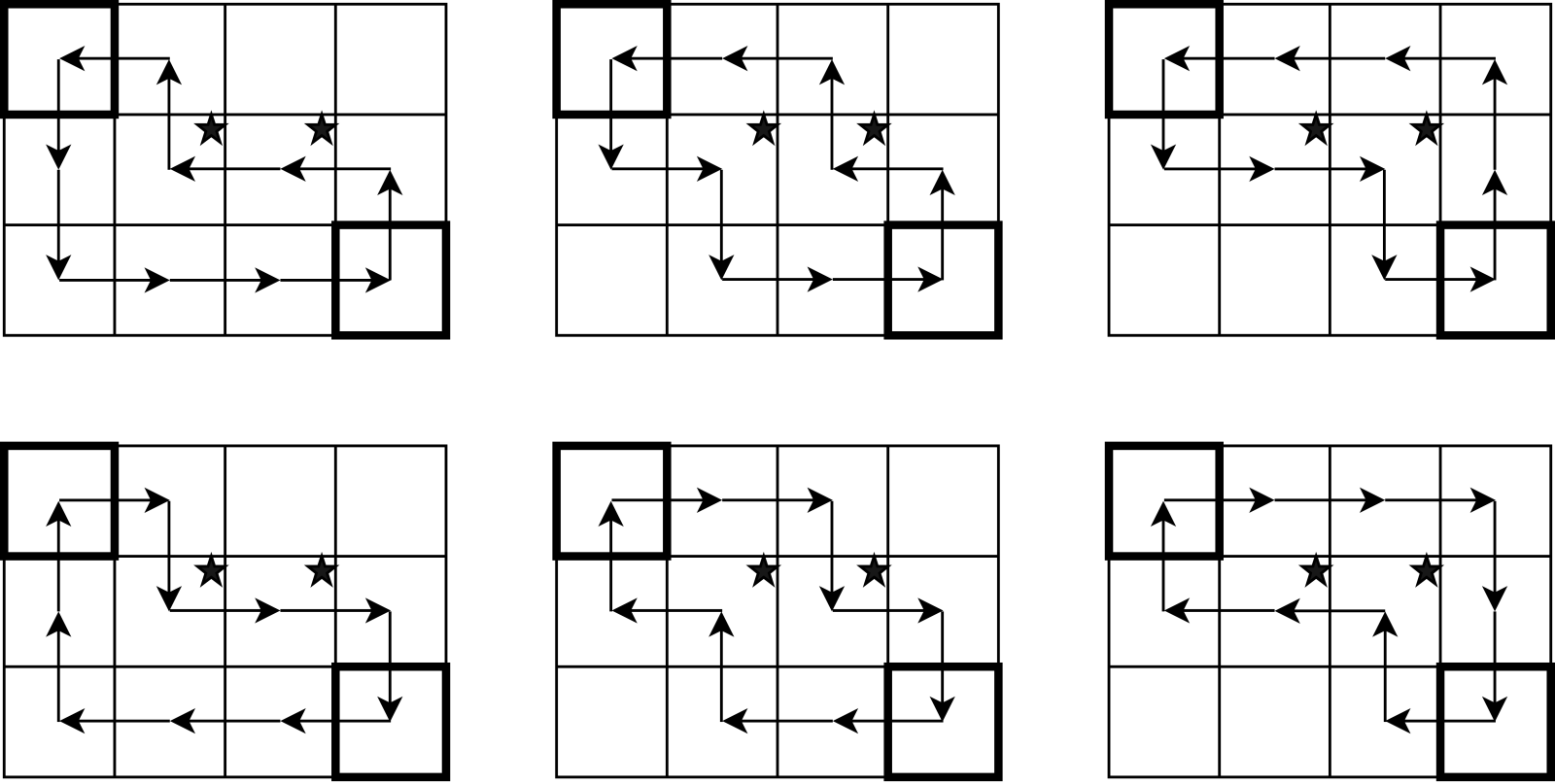
Клетки с достопримечательностями обозначены звездочкой.
Ваш ответ: