Задача: Беспилотная аэрологистика
На всероссийской олимпиаде по информатике 2224 года, которая проходит в Иннополисе, доставкой занимаются роботы нового поколения, которые способны создавать своих клонов. Доставку можно получить прямо через окно, не выходя из дома.
Изначально есть только один робот-доставщик. В любой момент верхний робот может создать одного или нескольких новых роботов прямо над собой. Так образуется колонна роботов. Высота каждого робота равна высоте одного этажа.

В процессе доставки колонна одинаковых роботов-клонов перемещается вдоль корпусов общежития слева направо. В базе данных у роботов содержится список сделанных заказов, для каждого из которых известно окно, в которое его нужно доставить. Когда колонна роботов проходит мимо окна, соответствующего какому-то заказу, она может произвести доставку, если в колонне есть робот, расположенный на уровне окна.

Во время перемещения конструкция из роботов может натолкнуться на препятствие. После препятствия движение продолжают только те экземпляры роботов, которые находились выше препятствия. Они оказываются на земле непосредственно за препятствием, по прежнему в виде вертикальной колонны, и могут продолжать движение, создавать новых клонов и доставлять заказы.

Расстояние между препятствиями и окнами достаточно большое, поэтому во время переезда через препятствие роботы не будут проезжать мимо окна.
За доставку одного заказа компания-организатор доставки получает \(p\) крипторублей. Стоимость создания одного нового робота равна \(c\) крипторублей. Итоговая прибыль равна суммарному доходу от доставки заказов за вычетом суммарной стоимости создания всех роботов. Компания хочет максимизировать свою прибыль. При этом, она не обязана выполнить все заказы, а роботы могут в любой момент остановиться, и прекратить процесс доставки.
Определите максимальную прибыль, которую может получить компания.
Формат входных данных
В первой строке входных данных находятся четыре целых числа \(n\), \(m\), \(c\), \(p\) (\(0 \le n, m \le 100\,000\), \(1 \le c, p \le 10^6\)) — количество препятствий, количество заказов в базе, стоимость создания клона робота и стоимость доставки одного заказа, соответственно.
В следующих \(n+m\) строках идёт описание препятствий и окон, в которые нужно доставить заказы, в порядке следования колонны роботов вдоль общежитий слева направо. Каждая строка содержит два целых числа \(t_i\) и \(h_i\) (\(1 \le t_i \le 2\), \(1 \le h_i \le 10^6\)) — тип объекта \(t_i\) (\(1\) для препятствия и \(2\) для окна) и \(h_i\) "— высота препятствия в этажах или этаж, на котором находится окно.
Гарантируется, что ровно \(n\) объектов имеют тип \(1\), и оставшиеся \(m\) объектов имеют тип \(2\).
Формат выходных данных
Выведите одно число — максимальную величину прибыли, которую можно получить.Одна из оптимальных стратегий доставки заказов из первого примера изображена на девяти рисунках ниже, при этом выполнение второго заказа не увеличивает прибыль.
Пояснения к примерам
Одна из оптимальных стратегий доставки заказов из первого примера изображена на девяти рисунках ниже, при этом выполнение второго заказа не увеличивает прибыль.
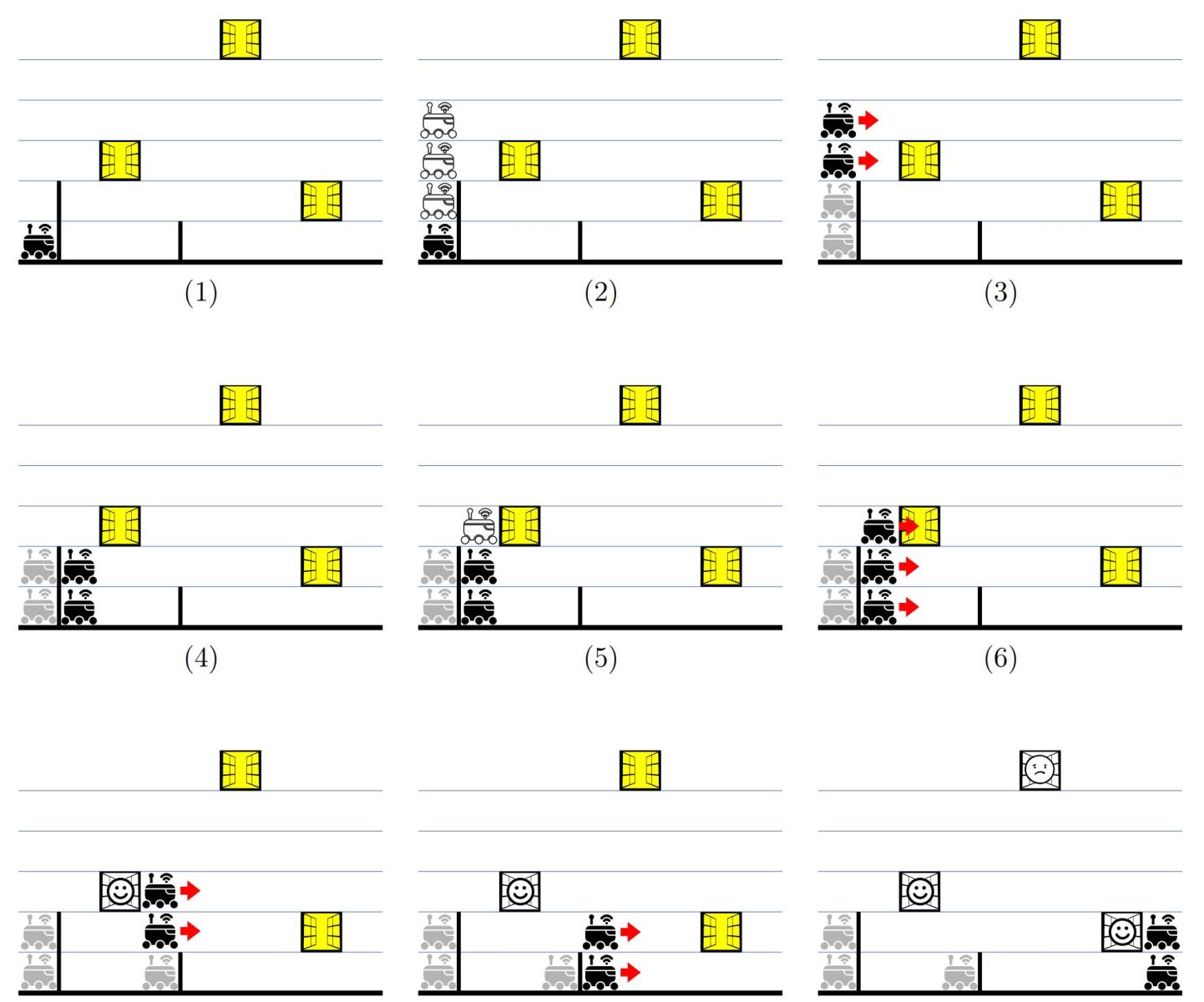
Во втором примере достаточно один раз клонировать робота для доставки первого заказа, полученной системой роботов доставить второй заказ, а производить дополнительное клонирование для доставки третьего заказа экономически невыгодно.
Ваш ответ: