Задача: Рамазан и капуста
Рамазан решил заняться серьезным бизнесом — выращиванием капусты.
Поле для выращивания капусты представляет собой бесконечное клетчатое поле. В каждой клетке поля может быть посажен один кочан капусты.
Рамазан засадил только часть поля. Он запланировал использовать несколько прямоугольных участков поля, причём оказалось, что некоторые из них могут пересекаться. Клетка поля принадлежит посадкам, если она лежит хотя бы в одном из прямоугольников.
Формально, Рамазан выбрал \(n\) прямоугольных участков \((x_i^{L}, y_i^{L}, x_i^{R}, y_i^{R})\) (\(x_i^{L} \leq x_i^{R}\), \(y_i^{L} \leq y_i^{R}\), \(1 \leq i \leq n\)). Клетка \((x, y)\) содержит капусту, если существует хотя бы один выбранный прямоугольник \(i\) (\(1 \leq i \leq n\)), такой что \(x_i^{L} \leq x \leq x_i^{R}\) и \(y_i^{L} \leq y \leq y_i^{R}\).
В прошлом Рамазан был программистом (и победителем), поэтому он решил использовать роботов с искусственным интеллектом для периодической обработки посадок. Один робот может обслуживать произвольный горизонтальный участок клеток \((x_1^{robot}, x_2^{robot}, y^{robot})\), то есть все клетки \((x, y)\), такие что \(x_1^{robot} \leq x \leq x_2^{robot}\) и \(y = y^{robot}\).
Важно, чтобы роботы ездили только по участкам с посадками. Он понял, что для минимизации количества роботов важно использовать горизонтальные участки, которые нельзя расширить. Рамазан будет использовать робота на участке клеток \((x_1^{robot}, x_2^{robot}, y^{robot})\), если:
-
Все клетки \((x, y)\), такие что \(x_1^{robot} \leq x \leq x_2^{robot}\) и \(y = y^{robot}\) принадлежат посадкам;
-
Клетка \((x_1^{robot} - 1, y^{robot})\) не принадлежит посадкам;
-
Клетка \((x_2^{robot} + 1, y^{robot})\) не принадлежит посадкам.
Ваша задача собрать важную статистику о роботах, которые будут работать на плантации. Будем говорить, что пара \((x_1, x_2)\) обслуживается в ряду \(y\), если существует робот, работающий ровно на участке \((x_1, x_2, y)\).
-
Найдите все пары \((x_1, x_2)\), которые обслуживаются в каком-нибудь ряду.
-
Для каждой такой пары \((x_1, x_2)\) найдите количество рядов, в которых она обслуживается.
-
Для каждой такой пары \((x_1, x_2)\) найдите максимальное количество подряд идущих рядов, в которых она обслуживается. Другими словами, найдите максимальное число \(k\), такое что существует отрезок \(k\) подряд идущих рядов \([y_1, y_2]\) (\(y_2 - y_1 + 1 = k\)), такой что для любого ряда \(y_1 \leq y \leq y_2\), пара \((x_1, x_2)\) обслуживается в ряду \(y\).
Формат входных данных
Каждый тест состоит из нескольких наборов входных данных. В первой строке дано одно целое число \(t\) (\(1 \leq t \leq 200\,000\)) — количество наборов входных данных. Далее следуют описания наборов входных данных.
В первой строке каждого набора входных данных дано единственное целое число \(n\) (\(1 \leq n \leq 200\,000\)) — количество выбранных прямоугольных участков.
В следующих \(n\) строках дано по четыре целых числа \(x_i^{L}\), \(y_i^{L}\), \(x_i^{R}\), \(y_i^{R}\) (\(1 \leq x_i^{L} \leq x_i^{R} \leq 10^9\), \(1 \leq y_i^{L} \leq y_i^{R} \leq 10^9\)) — описания выбранных прямоугольных участков.
Обозначим за \(N\) сумму \(n\) по всем наборам входных данных в одном тесте. Гарантируется, что \(N \leq 200\,000\).
Формат выходных данных
Для каждого набора входных данных сначала выведите единственное целое число \(p\) (\(p \geq 1\)) — количество пар \((x_1, x_2)\), которые обслуживаются в каком-нибудь ряду.
В следующих \(p\) строках выведите по четыре целых числа \(x_1\), \(x_2\), \(cnt\), \(k\) (\(1 \leq x_1 \leq x_2 \leq 10^9\), \(0 \leq cnt, k \leq 10^9\)). Число \(cnt\) должно быть равно количеству рядов, в которых обслуживается пара \((x_1, x_2)\). Число \(k\) должно быть равно максимальному количеству подряд идущих рядов, в которых обслуживается пара \((x_1, x_2)\).
Все пары \((x_1, x_2)\) должны быть различны. Каждая пара, которая обслуживается в каком-нибудь ряду, должна быть выведена ровно один раз. Можно вывести пары в произвольном порядке.
Система оценки
Для набора входных данных обозначим за \(w\) ширину поля, то есть \(w = \max\limits_{i=1}^{n} x_i^{R}\), за \(h\) высоту поля, то есть \(h = \max\limits_{i=1}^{n} y_i^{R}\).
| 3-5 [0cm][0cm]Подз. |
[0cm][0cm]Баллы |
\(n\), \(N\) |
\(w, h\) |
дополнительно |
[0cm][0cm]
Необх. подзадачи
|
|
| 1 |
4 |
\(n = 1\) |
|
|
|
|
| 2 |
8 |
|
\(h = 1\) |
|
|
|
| 3 |
8 |
\(n \leq 30\), \(N \leq 3000\) |
\(w, h \leq 10\) |
\(t \leq 100\) |
У |
|
| 4 |
4 |
|
\(w, h \leq 5000\), \(\sum wh \leq 25 \cdot 10^6\) |
|
У, 3 |
|
| 5 |
8 |
\(N \leq 3000\) |
|
|
У, 3 |
|
| 6 |
4 |
\(N \leq 10\,000\) |
|
|
У, 3, 5 |
|
| 7 |
8 |
|
|
все \([x_i^{L}, x_i^{R}]\) пересекаются |
1 |
|
| 8 |
8 |
|
|
\(y_i^{L} = 1\) |
2 |
|
| 9 |
8 |
|
|
прямоугольники не пересекаются |
1 |
|
| 10 |
8 |
|
|
\(\forall 1 \leq i, j \leq n\) \(\forall y \in [y_i^{L}, y_i^{R}] \cap [y_j^{L}, y_j^{R}]\) выполнено \([x_i^{L}, x_i^{R}] \nsubseteq [x_j^{L}, x_j^{R}]\) |
1, 9 |
|
| 11 |
8 |
|
|
все отрезки \([x_i^{L}, x_i^{R}+1]\) либо вложены, либо не пересекаются |
1 |
|
| 12 |
8 |
\(N \leq 50\,000\) |
|
|
У, 3, 5 – 6 |
|
| 13 |
8 |
\(N \leq 100\,000\) |
|
|
У, 3, 5 – 6, 12 |
|
| 14 |
8 |
\(N \leq 200\,000\) |
|
|
У, 1 – 13 |
|
-
Если для теста ваше решение неправильно находит множество пар \((x_1, x_2)\), которые обслуживаются в каком-нибудь ряду, решение получает вердикт <<Неправильный ответ>>.
-
Если во всех тестах подзадачи и необходимых подзадач решение
-
правильно находит множество, но не все \(cnt\) верны, оно получает \(50\%\) баллов за подзадачу.
-
правильно находит множество и все \(cnt\), но не все \(k\) верны, оно получает \(75\%\) баллов за подзадачу.
-
правильно находит множество, все \(cnt\) и все \(k\), оно получает \(100\%\) баллов за подзадачу.
Обратите внимание, что для получения частичных баллов за подзадачу, все равно необходимо вывести какие-нибудь значения \(cnt\) и \(k\) для каждой пары \((x_1, x_2)\), но не обязательно верные.
Пояснения к примерам
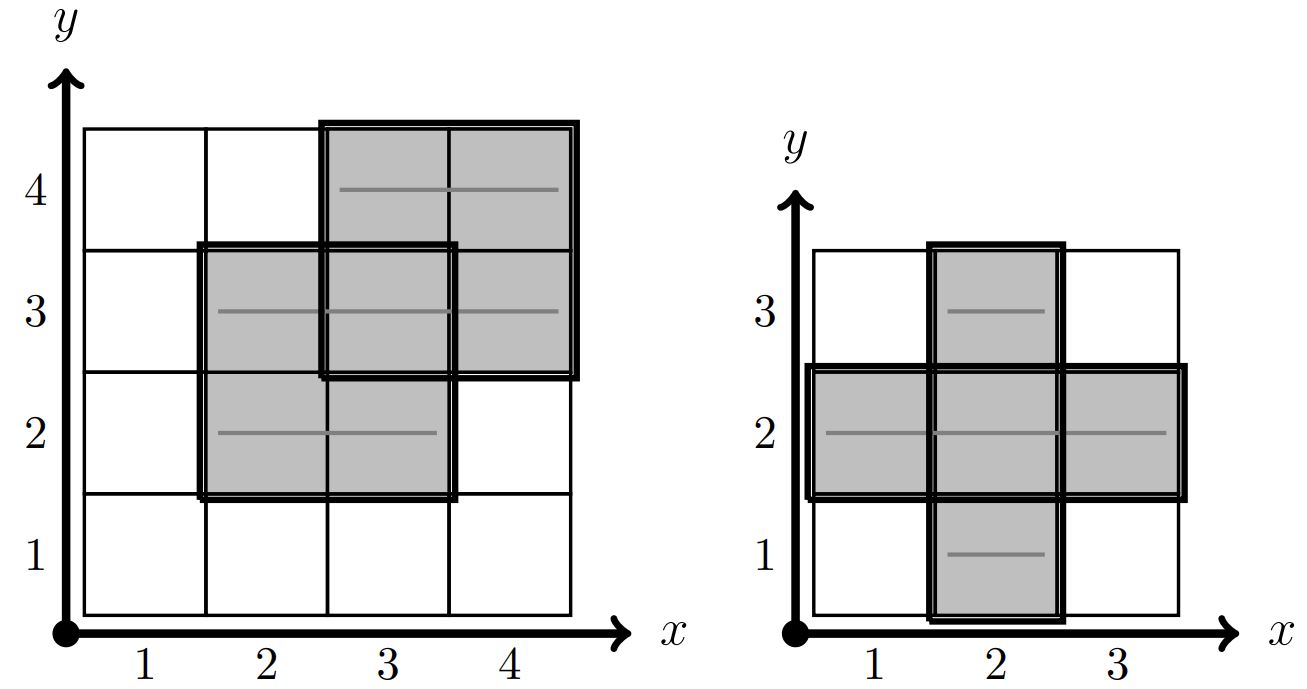
Первый и второй наборы входных данных для теста из условия
В первом наборе входных данных будут использоваться роботы на участках \((2, 3, 2)\), \((2, 4, 3)\), \((3, 4, 4)\). Таким образом, пары \((2, 3)\), \((2, 4)\), \((3, 4)\) обслуживаются в каком-нибудь ряду, причем каждая из них обслуживается ровно в одном ряду.
Во втором наборе входных данных будут использоваться роботы на участках \((2, 2, 1)\), \((2, 4, 2)\), \((2, 2, 3)\). Таким образом, пары \((2, 2)\), \((2, 4)\) обслуживаются в каком-нибудь ряду. Пара \((2, 2)\) обслуживается в рядах \(1, 3\), пара \((2, 4)\) обслуживается ряду \(2\).
Третий и четвертый наборы входных данных для теста из условия
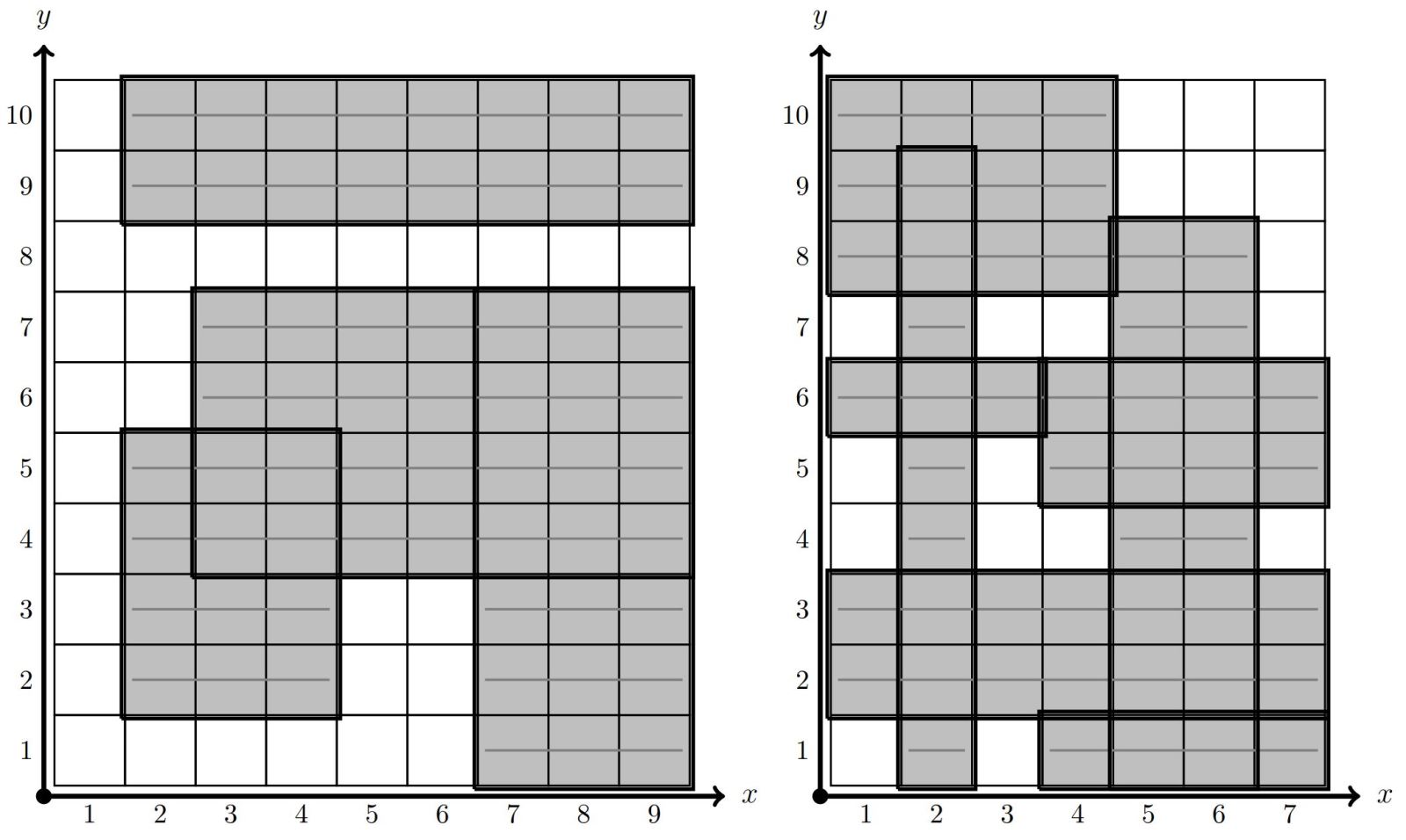
Ваш ответ: