Гномы продолжают искать золото предков в недрах Одинокой горы. Недра Одинокой горы представляют собой n пещер, некоторые из которых соединены двусторонними переходами. При этом из каждой пещеры в любую другую можно попасть по переходам, причем это можно сделать единственным способом.
Гномы разделились на два отряда, которые начали свои поиски с пещер u
0 и v
0, соответственно. Гномы каждого из отрядов перемещаются вместе. На обследование пещеры у отряда гномов уходит ровно одна минута, после чего каждый отряд быстро перемещается по переходу в одну из соседних пещер. При этом гномы никогда не заходят в пещеру, если они или другой отряд в ней уже побывали. Оба отряда никогда не заходят в одну и ту же пещеру. Если хотя бы один из отрядов гномов не может переместиться в соответствии с этими правилами, оба отряда сразу прекращают поиски сокровищ.
Чтобы как можно лучше обследовать недра Одинокой горы, гномы хотят, чтобы поиски продолжались как можно дольше. По заданной карте пещер в Одинокой горе и начальному положению отрядов гномов определите, какое максимальное время могут продолжаться поиски сокровищ.
Формат входных данных
В первой строке число n (2 ≤ n ≤ 200 000) — число пещер в Одинокой горе. В следующих n−1 строках заданы переходы между пещерами. В каждой строке записаны номера двух пещер v и u, соединенных переходом (1 ≤ v, u ≤ n). В следующей строке заданы номера пещер v
0 и u
0, в которых исходно находятся два отряда гномов (1 ≤ v
0, u
0 ≤ n, v
0 != u
0).
Формат выходных данных
Выведите максимальное число минут, которое могут продолжаться поиски сокровищ.
| Ввод |
Вывод |
Пояснение |
6
1 2
2 3
3 4
4 5
5 6
4 5 |
2 |
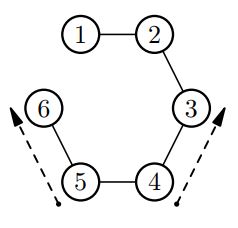 |
8
1 2
2 3
3 4
2 5
5 6
3 7
7 8
1 8 |
4 |
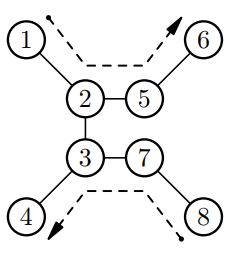 |