Модуль: Алгоритм Флойда


1. Флойд: Начало (C++)

☰ Теория

Дан ориентированный или неориентированный взвешенный граф с n вершинами.
Алгоритм позволяет найти расстояние от каждой до каждой вершины и работает с отрицательными ребрами.
 
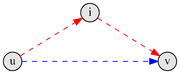
   Алгоритм последовательно перебирает все такие I, через которые может лежать более короткий путь в V, чем который имеется сейчас. 

Текущий (синий) путь и потенциально более короткий (красный).

Реализация
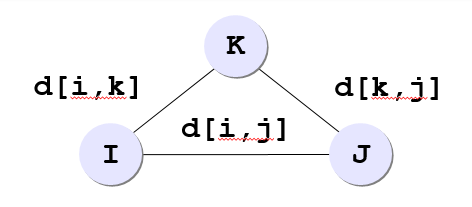
На вход программе подаётся граф, заданный в виде матрицы смежности — двумерного массива d[][] размера n х n, в котором каждый элемент задаёт длину ребра между соответствующими вершинами.
Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число ( например INT_MAX в "limits.h", чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно.
Но при сложении двух бесконечностей может получиться переполнение int и на выходе будем иметь какое то отрицательно значение, поэтому неплохо бы подстраховаться дополнительной проверкой:  
if (d[i][k] < INT_MAX && d[k][j] < INT_MAX)
В итоге алгоритм будет иметь вид:
  
for (int k=0; k<n; ++k)
	for (int i=0; i<n; ++i)
		for (int j=0; j<n; ++j)
			if (d[i][k] < INT_MAX && d[k][j] < INT_MAX)
				if(d[i][k]+d[k][j] < d[i][j])
                                     d[i][j] = d[i][k] + d[k][j];


Например, дан граф:



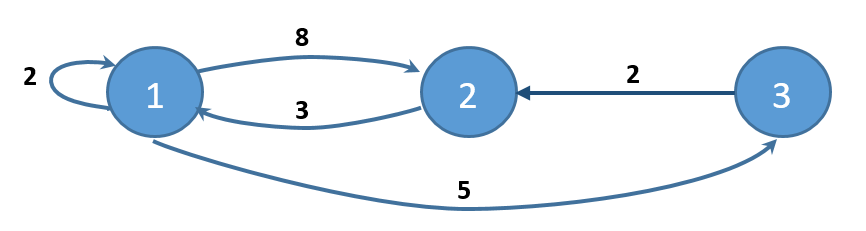
Тогда начальная весовая матрица будет:
номера вершин 1 2 3
1 0 8 5
2 3 0 INT_MAX
3 INT_MAX 2 0

после 1-ой итерации:
 
номера вершин 1 2 3
1 0 8 5
2 3 0 8
3 INT_MAX 2 0

после 2-ой итерации:
 
номера вершин 1 2 3
1 0 8 5
2 3 0 8
3 5 2 0


после 3-ей итерации:
 
номера вершин 1 2 3
1 0 7 5
2 3 0 8
3 5 2 0



 

Дан ориентированный граф, рёбрам которого приписаны некоторые неотрицательные веса (длины). Найти длину кратчайшего пути из вершины s в вершину t.
 
Входные данные
В первой строке заданы три числа: число вершин в графе N ≤50, номера вершин s и t. Далее идёт матрица смежности графа, то есть N строк, в каждой из которых записано N чисел. j-ое число в i-ой строке матрицы смежности задает длину ребра, ведущего из i-й вершину в j-ую. Длины могут принимать любые значения от 0 до 1000000, число -1 означает отсутствие соответствующего ребра. Гарантируется, что на главной диагонали матрицы стоят нули.
 
Выходные данные
Выведите одно число – минимальную длину пути. Если пути не существует, выведите -1.

Примеры
№ Входные данные Выходные данные
1
3 1 2
0 -1 3
7 0 1
2 215 0
 218
Вставьте недостающие фрагменты кода
C++ 
#include <vector>
#include <iostream>
#include <climits>
using namespace std;

const int inf = INT_MAX;

int main()
{
	int n, s, t;
	cin >> n >> s >> t;
	vector<vector<int> > d(n + 1, vector<int>(n + 1,inf));
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			int a;
			cin >> a;
			if (a != -1)
			{
				d[i + 1][j + 1] = a;
			}
		}
	}
	for (int k = 1; k <= n; ++k)
	{
		for (int i = 1; i <= n; ++i)
		{
			for (int j = 1; j <= n; ++j)
			{      
			}
		}
	}
	if (d[s][t] == inf)
	{
		cout << -1;
		return 0;
	}
	cout << d[s][t] << endl;

}
     

time 1000 ms
memory 32 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Комментарий учителя

Результат проверки программы 
Для проверки решения задачи необходимо зарегистрироваться или авторизоваться!