2.
Хранение взвешенных графов (C++)
Взвешенный граф
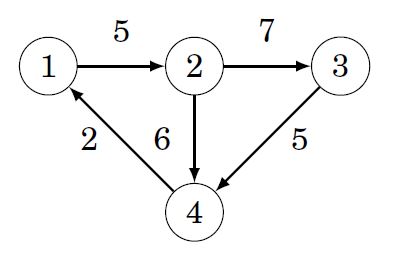
Во взвешенном графе, помимо самих ребер и их направления, каждое ребро обладает также весом или стоимостью. Существует несколько способов хранения списка вершин во взвешенном графе:
-
Матрица смежности. В этом способе граф представляется в виде двумерной матрицы, где строки и столбцы соответствуют вершинам графа, а элементы матрицы содержат информацию о весе ребер между вершинами. Если между вершинами нет ребра, то соответствующий элемент матрицы будет иметь значение "бесконечность" или другое специальное значение.
-
Список смежности. В этом способе каждая вершина представляется в виде списка, содержащего пары (или кортежи) вершин, с которыми она имеет ребра, и их соответствующие веса. Например, для вершины A список смежности может выглядеть как [(B, 5), (C, 3)], что означает наличие ребра с весом 5 к вершине B и ребра с весом 3 к вершине C.
-
Список ребер: В этом способе граф представляется в виде списка всех его ребер, где каждое ребро содержит информацию о вершинах, которые оно соединяет, и его весе. Например, [(A, B, 5), (A, C, 3)].
Выбор способа хранения зависит от конкретных требований и задачи, с которой вы работаете. Некоторые способы могут быть более эффективными для определенных операций, таких как поиск кратчайшего пути или обход графа.
По заданному изображению ориентированного графа сформируйте список смежных вершин для всех вершин. Вершины добавляйте в порядке возрастания.
Вставьте недостающие фрагменты кода
C++
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n, m, s, f;
const int V = 4;
vector< vector < pair <int, int>>> adj(V+1);
adj[1].push_back({ 2,5 });
// остальные ребра добавьте сами в порядке возрастания вершин
|
|
|
for (size_t i = 1; i <= V; i++)
{
cout << i << ": ";
for (auto x : adj[i])
cout << "-> " << x.first << "("<<x.second<<")";
cout << "\n";
}
return 0;
}
|