Модуль: Графы. BFS - обход в ширину


Задача

1/17

BFS: Начало (Python)

Теория Нажмите, чтобы прочитать/скрыть

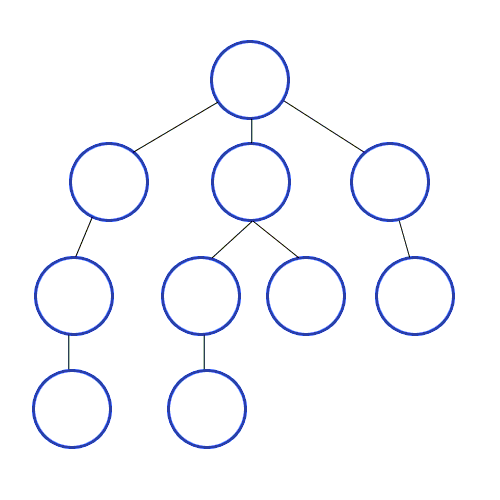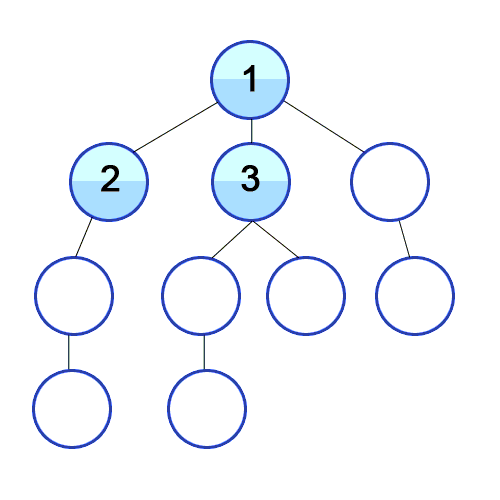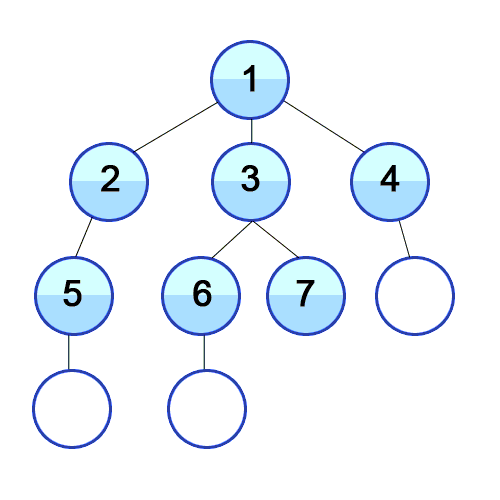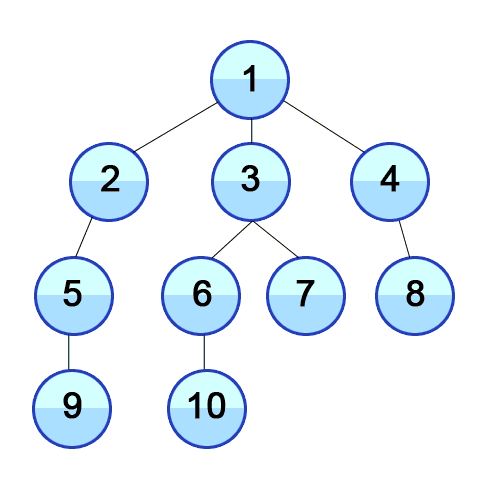
Breadth first search (BFS) - поиск в ширину

Стандартная реализация BFS относит каждую вершину графа к одной из двух категорий:
1. Посещенные
2. Не посещенные

Цель алгоритма - пометить каждую вершину как посещенную, избегая при этом циклов.
Алгоритм работает следующим образом:
  1. Начните с того, что поместите любую из вершин графа в конец очереди.
  2. Возьмите первый элемент очереди и добавьте его в список посещенных.
  3. Создайте список смежных вершин этой вершины. Добавьте в конец очереди те из них, которых нет в списке посещенных.
  4. Повторяйте шаги 2 и 3, пока очередь не станет пустой.
Граф может иметь две разные несвязные части, поэтому, чтобы убедиться, что мы покрываем каждую вершину, мы можем также запустить алгоритм BFS на каждой вершине.
Для написания простейшего BFS необходимо уметь работать с такой структурой данных, которая позволяет брать из начала и класть в конец (очередь), а также уметь хранить граф в виде списка.
 
Алгоритм работы на псевдокоде
BFS(G, start):
    // Инициализация очереди и множества посещенных вершин
    создать пустую очередь Q
    добавить start в Q
    создать массив посещенных вершин visited (visited[i] = True, если посетили вершину i, иначе False)
    добавить start в visited
    
    // Пока очередь не пуста
    пока Q не пуста:
        Извлекаем вершину из очереди - она будет текущей
        Удаляем текущую_вершину из очереди 
        
        // Для каждой смежной вершины, которая не была посещена
        для каждой смежной_вершины от текущей вершины:
            если смежная_вершина не содержится в visited:
                добавить смежную_вершину в Q
                отметить смежную_вершину в visited

В качестве посещенных вершин можно брать не массив, а множество.


Сложность работы
Так как в худшем случае алгоритм посещает все узлы графа, при хранении графа в виде списков смежности, временная сложность алгоритма составляет O(|V| + |E|), где V - множество вершин графа, а E - множество ребер. Другими словами, алгоритм в худшем случае работает за количество ребер + количество вершин.


Алгоритм поиска в ширину (BFS) является одним из фундаментальных алгоритмов обхода графа и находит широкое применение во многих областях: 
  • Поиск кратчайшего пути между двумя вершинами в невзвешенном графе. Это может быть использовано, например, для поиска кратчайшего пути в лабиринте или для определения минимального количества ходов, необходимых для достижения цели.
  • Поиск в ширину: BFS используется для обхода графа в ширину, что означает, что он посещает все вершины на одной уровне перед переходом к следующему уровню. Это может быть полезно, например, при поиске всех соседей вершины или при проверке связности графа.
  • Поиск в графе: BFS может использоваться для поиска конкретной вершины или проверки ее наличия в графе. Он также может быть применен для поиска всех возможных путей от стартовой вершины до целевой вершины.
  • Поиск компонент связности: BFS позволяет найти все вершины, достижимые из данной стартовой вершины, и таким образом определить компоненты связности в графе.
  • Поиск взвешенных кратчайших путей: Хотя BFS обычно используется для невзвешенных графов, он может быть модифицирован для поиска кратчайших путей во взвешенных графах с неотрицательными весами ребер (например, использованием алгоритма Dijkstra).
 
 

Задача

Некоторые деревни соединены между собой дорогами, которые можно представить в виде неориентированного графа. Вершины данного графа - это деревни, а ребра - дороги между деревнями (граф может содержать циклы). Известно, что в деревне S основана артель коробейников. Каждое утро, чтобы продать свою мелкую галантерею, коробейники выходят в деревни, которые еще не посетили, и в которые есть дорога из текущей. Артель коробейников всегда делится на группы так, чтобы они могли за один день обойти все деревни, которые имеют дороги из текущей.
За сколько дней коробейники посетят все деревни?
Напишите функцию \(bfs()\), которая будет возвращать ответ на задачу.


Входные данные
В первой строке вводятся 3 целых числа n, m, s (\(1 <= n <= 10^5\), \(0 <= m <= 10^5\), \(1 <= s <= n\)) - количество деревень, количество дорог между ними и номер деревни, в которой основана артель коробейников. В следующих m строках содержится по 2 числа u, v(\(1 <= u, v <= n\)) - номера двух деревень, между которыми есть дорога. Индексация деревень ведется с 1.

Выходные данные
Выведите одно число - за сколько дней коробейники посетят все деревни.
 
 
Примеры
№ Входные данные Выходные данные
1 6 7 1
1 2
1 5
2 3
5 4
3 4
3 6
4 6		 4

time 1000 ms
memory 32 Mb
Правила оформления программ и список ошибок при автоматической проверке задач

Комментарий учителя

Вставьте недостающие фрагменты кода
Python
Напишите программу ниже 
def bfs():                 
n, m, s = map(int, input().split())
s  -=  1
visited = [False] * n  # True, если были в вершине i
tm = [0] * n    # tm[i] - день, когда в деревню i пришла артель коробейников
g = []     # список смежности
for i in range(n):
    g.append([])


for i in range(m):
    u, v = map(int, input().split())
    u -= 1
    v -= 1
    g[u].append(v)
    g[v].append(u)

print(bfs())

     

Результат проверки программы 
Для проверки решения задачи необходимо зарегистрироваться или авторизоваться!