Дерево отрезков
Дерево отрезков (ДО) — это структура данных, которая позволяет эффективно (т.е. за асимптотику O (log n)) реализовать операции следующего вида:
- нахождение суммы/минимума элементов массива в заданном отрезке (a[l...r], где l и r поступают на вход алгоритма),
- изменение элементов массива: как изменение значения одного элемента, так и изменение элементов на целом подотрезке массива (т.е. разрешается присвоить всем элементам a[l...r] какое-либо значение, либо прибавить ко всем элементам массива a[l...r] какое-либо число).
ДО можно писать или на отрезках или на полуинтервалах,то есть вершина будет хранить какую-нибудь функцию на отрезке
[l;r],если писать на отрезках или на полуинтервале
[l;r), если писать
на полуинтервалах. Большой разницы нет, в этой статье объяснение будет на полуинтервалах.
Давайте разберем ДО на примере суммы на отрезке и прибавления на отрезке.
Разобьём начальный массив размера
n на две примерно равные половинки:
[0;n/2) и
[n/2;n). Данные половинки разобьём так же на половинки. И так пока не дойдем до размера 1. При этом считаем функцию на всех этих половинках, размера
n,
n/2,
n/4 и т.д.Так будет выглядеть дерево для массива
{1, -5, 6, 10}. Сверху вершины указаны границы ее поддерева, в самой вершине сумма.
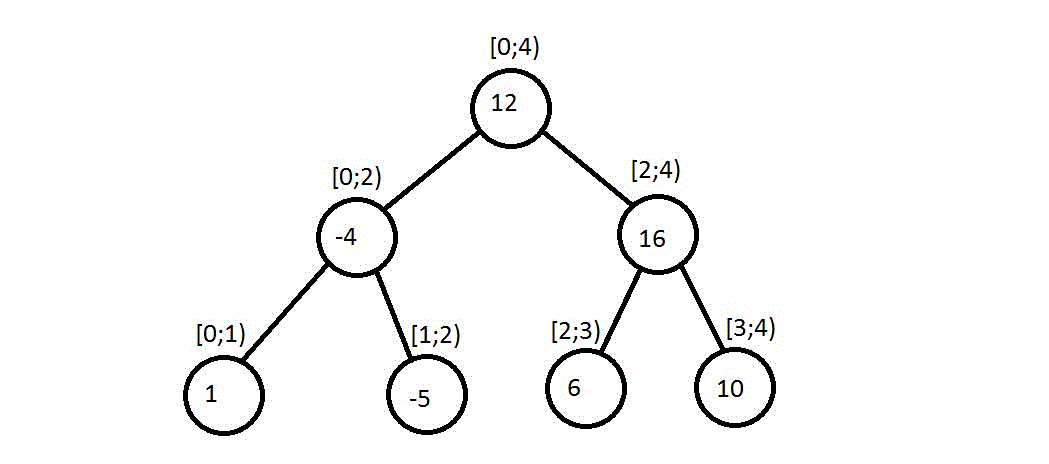
Из рисунка видно, чтобы посчитать функцию в текущей вершине надо пересчитать через функции от детей. Например, сумма в текущей вершине – это сумма в левом ребенке + сумма в правом ребенке. Минимум в текущей вершине – это минимум из минимумов детей и т.п.
Так же есть небольшое неудобство, если размер массива это не степень двойки, тогда дерево не будет таким “идеальным”. Но на практике это никакого неудобства не приносит.
Теперь обратимся к коду и реализации такого дерева.
Давайте заведем структуру
Node, в которой будем хранить границы ее поддерева, функцию на поддереве (например, сумму), ссылки на ее детей (как это реализовать будет чуть позже), и поле
add,в котором будем хранить сколько нужно прибавить ко всем элементам поддерева (чуть позже объясняется зачем это нужно). В коде это выглядит примерно так. (Если кто не знает поле – это переменная в структуре).
struct Node {
Node* left;
Node* right;
int lb, rb, sum, add;
};
Поля
Node* left; и
Node* right; это указатели на левого и правого сыновей соответственно.Поля
int lb,
int rb границы вершины,
sum – сумма на подмассива
[lb;rb), поле
add объясняется чуть позже.
Но есть один вопрос: что делать с листами дерева, у них же нет сыновей? Следовательно придется проверять и пересчитывать функцию не через детей, а просто забивать элемент массива (так как границы у листа
[i;i+1)). Давайте вместо этого создадим фиктивную вершину, в которой в поле результата функции будет какой-нибудь нейтральный элемент (для суммы это 0, для произведения 1, для минимума бесконечность).
Код
Node* Empty = new Node({ NULL, NULL, 0, 0, 0, 0 });
Кто не знает,
{} означает конструктор, то есть, таким образом создается указатель на структуру у которой поля
left и
right равны
NULL, поля
lb,
rb,
sum,
add равны
0.
NULL - указатель на пустоту.
Теперь, после создания самой вершины, давайте построим из них само дерево. Напишем функцию
build, которая будет собственно строить саму структуру дерево, пока без подсчета функции.
Будем делать это следующим образом: будем рекурсивно передавать в функцию границы текущей вершины. Если наша текущая вершина лист,то давайте вернем новую вершину, границы в которой будут нашими текущими границами, сумма 0, поле
add так же 0 (нам ничего пока что прибавлять не нужно), а дети-фиктивные вершины, то есть
Empty. Если же текущая вершина не лист, то давайте запустим нашу функцию
build(l, mid) и
build(mid, r), где
mid = (l + r) / 2. Таким образом, мы построим сыновей текущей вершины. После построения вернем вершину, у которой левый ребенок будет результат выполнения
build(l, mid), правый ребенок результатом выполнения
build(mid, r), поля
lb и
rb нашими текущими вершинами, а поля
sum и
add так же 0.
Код
Node* build(int l, int r) {
if (l + 1 == r) { // проверка на то, что вершина - лист
return new Node ({ Empty, Empty, l, r, 0, 0});
}
int mid = (l + r) / 2;
Node* nleft = build(l, mid); // построение левого сына
Node* nright = build(mid, r); // построение правого сына
return new Node({ nleft, nright, l, r, 0, 0 });
}
Например, так будет выглядеть дерево при массиве размера 4. То есть мы запустим функцию
build(0, 4).
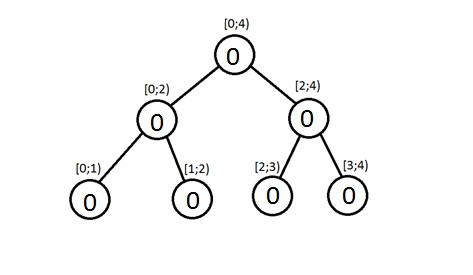
Теперь давайте посчитаем асимптотику функции
build для массива размера
n.
Как было описано ранее начальный массив мы поделим на 2 примерно равные части,затем эти части на еще 2 и так далее, пока не дойдем до размера 1. Сколько раз мы поделим отрезки на 2? Очевидно, что
log(n). Следовательно высота нашего дерева будет не больше
log(n), и на каждом уровне не больше
n вершин, следовательно итоговая асимптотика
O(nlogn).
Теперь нам надо изменить наши значения в дереве. Можно это делать вручную, просто рекурсивно спускаться по дереву и когда дошли до листа, то присвоить ему элемент соответствующий ему в массиве, а когда будем возвращаться рекурсивно обратно, пересчитывать функцию в текущей вершине.
Код
// v - текущая вершина,
// ind - индекс элемента, к которому надо прибавить,
// d - что прибавить
void change(Node* v, int ind, int d){
if (v->rb <= ind || v->lb > ind)
{
// если мы зашли в вершину, в поддереве которой
// точно нет элемента с номером ind, то дальше идти нет смысла
return;
}
if (v->lb + 1 == v->rb)
{
// если дошли до листа, то прибавляем к его значению d
// и заканчиваем
v->sum += d;
return;
}
change(v->left, ind, d); // запуск от левого сына
change(v->right, ind, d); // запуск от правого сына
v->sum = v->left->sum + v->right->sum; // пересчет функций от детей
}
Асимптотика так же будет
log(n), так как высота не больше
log(n).
Давайте попробуем реализовать массовое прибавление на полуинтервале
[l;r) за асимптотику
log(n).Тогда прибавление к одному элементу мы сможем делать как массовое прибавление на отрезке длины 1. Для этого нам и пригодится поле
add. Будем делать следующее: нам пришел запрос прибавления на полуинтервале
[l;r) числа
d. Давайте не будем честно идти и прибавлять на всем полуинтервале число
d, а будем просто запоминать, что мы должны прибавить. Поле
add и будет отвечать за данное запоминание.
Для начала реализуем такую функцию, которая бы “проталкивала” информацию о прибавлении детям данной вершины. Так как, если нашей текущей вершине надо что-то прибавить, то и ее детям надо прибавить абсолютно тоже самое (это видно из структуры самого дерева). Так же в этой функции будем сразу пересчитывать функцию всего поддерева. Это делается довольно очевидно. Как изменится сумма на отрезке размера
size, если ко всем его элементам прибавится одно и тоже число
d? Логично, что прибавиться
d*size. Если бы мы считали не сумму, то пересчет выводился бы в зависимости от функции. Например,если бы был минимум, то к минимуму бы просто прибавилось число
d.
Код
void push(Node* v)
{
if (v == Empy)
{
// если мы зашли в фиктивную вершину,
// то "проталкивать" нам некуда,
// так что просто ничего не делаем
return;
}
v->sum += v->add * (v->rb - v->lb); // пересчет функции
v->left->add += v->add; // "проталкивание" информации в левого ребенка
v->right->add += v->add; // "проталкивание" в правого
v->add = 0; // мы уже обновили текущую вершину, так что помнить нам больше не нужно
}
Теперь приведу саму функцию прибавления на отрезке:
void change(Node* v, int l, int r, int d)
{
push(v); // проталкиваем информацию
if (v->lb >= r || v->rb <= l)
{
// если отрезки нашей вершины и отрезка
// пересекаются, то дальше нет смысла идти,
// так как ничего менять не надо
return;
}
if (l <= v->lb && r >= v->rb)
{
// если отрезок нашей вершины
// лежит в отрезке запроса, то нам надо поменять значения
// во всем поддереве
v->add += d;
push(v);
return;
}
// если не выполнились первые два условия, то
// надо спуститься ниже
change(v->left, l, r, d);
change(v->right, l, r, d);
if (v == Empty)
{
return;
}
v->sum = v->left->sum + v->right->sum; // пересчет функции от детей
}
Асимптотика данной функции
O(logn).