Степени вершин
Степенью вершины называется количество ребер, которые связаны с этой вершиной.
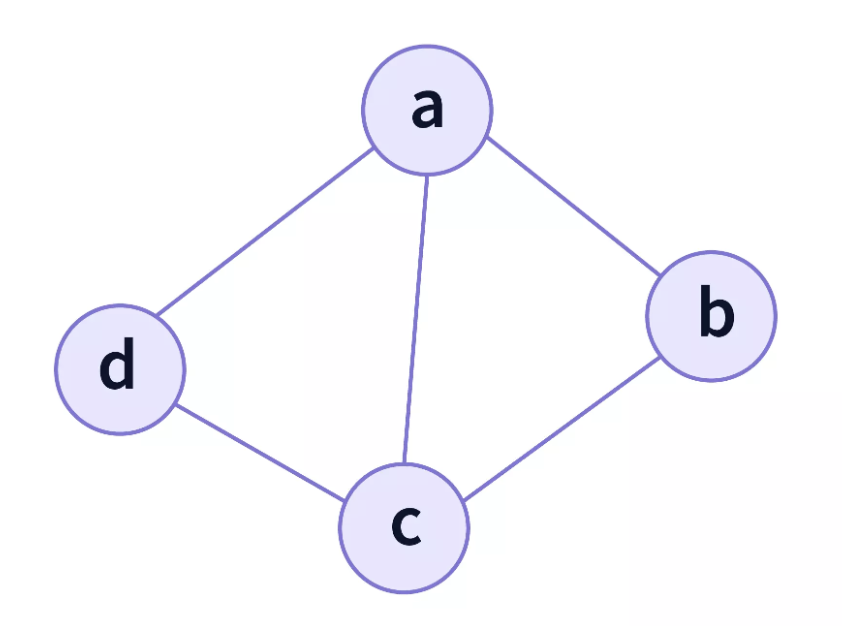 Рассмотрим следующий граф, изображенный на рисунке слева.
Рассмотрим следующий граф, изображенный на рисунке слева.
Если мы посмотрим на вершину a, то у нее есть три ребра (одно соединяет a с b, другое - с c, третье - с d ). Значит, степень вершины a равна 3.
Теперь давайте проверим степени остальных вершин. У вершины b есть два ребра, поэтому степень вершины b равна 2. А у вершины c есть также как и у a три ребра, значит, степень вершины с равна 3, степень вершины d равна двум.
Мы можем также посчитать сумму степеней всех вершин в графе. В данном случае, сумма степеней равна
3 + 2 + 3 + 2 = 10.
И вот интересный факт: сумма степеней всех вершин всегда равна двойному количеству ребер в графе! В нашем примере у нас 5 ребер, и сумма степеней вершин действительно равна 10.
Также есть еще одна забавная штука, которую называют "леммой о рукопожатиях". Если представить, что каждое ребро - это рукопожатие между двумя людьми, то в любой компании количество людей, сделавших нечетное число рукопожатий, всегда будет четным. В нашем графе таких вершин две (a и с).