Двумерное динамическое программирование
Двумерное динамическое программирование (2D DP) - это метод решения задач, которые имеют два изменяемых параметра и часто используются для оптимизации.
Рассмотрим этот метод на примере задачи о нахождении минимального пути в сетке.
Задача
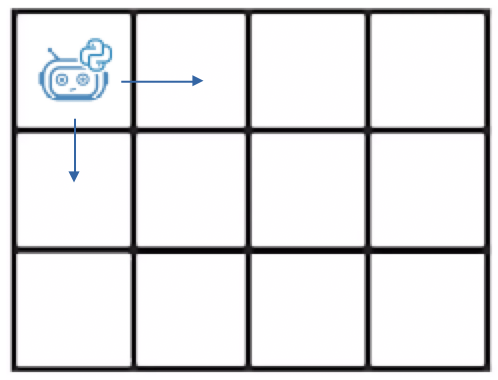 В левом верхнем углу прямоугольной сетки размером
В левом верхнем углу прямоугольной сетки размером NxM расположен робот. Он хочет добраться до правого нижнего угла. При этом, он может передвигаться только на одну клетку вниз или на одну клетку вправо. Найдите количество различных путей, по которым робот может попасть в правый нижний угол.
Будем решать задачу, используя план решения задач на динамическое программирование:
1) Решим задачу для маленьких значений
- Если сетка состоит только из 1 строки, то количество путей, попасть в любую клетку равно одному (
a1,m = 1).
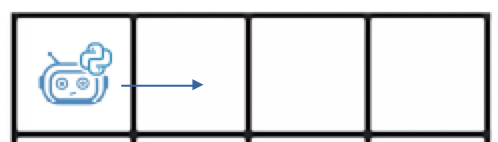
- Если сетка состоит из 1 столбца, то количество способов также будет равно одному (
an,1 = 1).
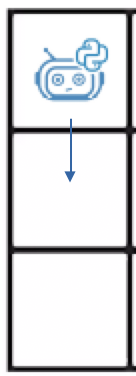
- если сетка 2x2, то количество путей будет равно двум. Каждый вариант указан стрелкой на рисунке.
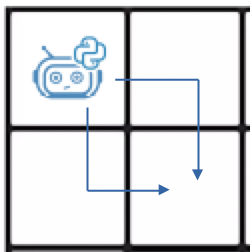
2. Введем обозначение:
ai,j- количество различных путей попасть из клетки с координатой
(1, 1) в клетку с координатой
(i, j).
3. Составим рекуррентную формулу для вычисления
ai,j.
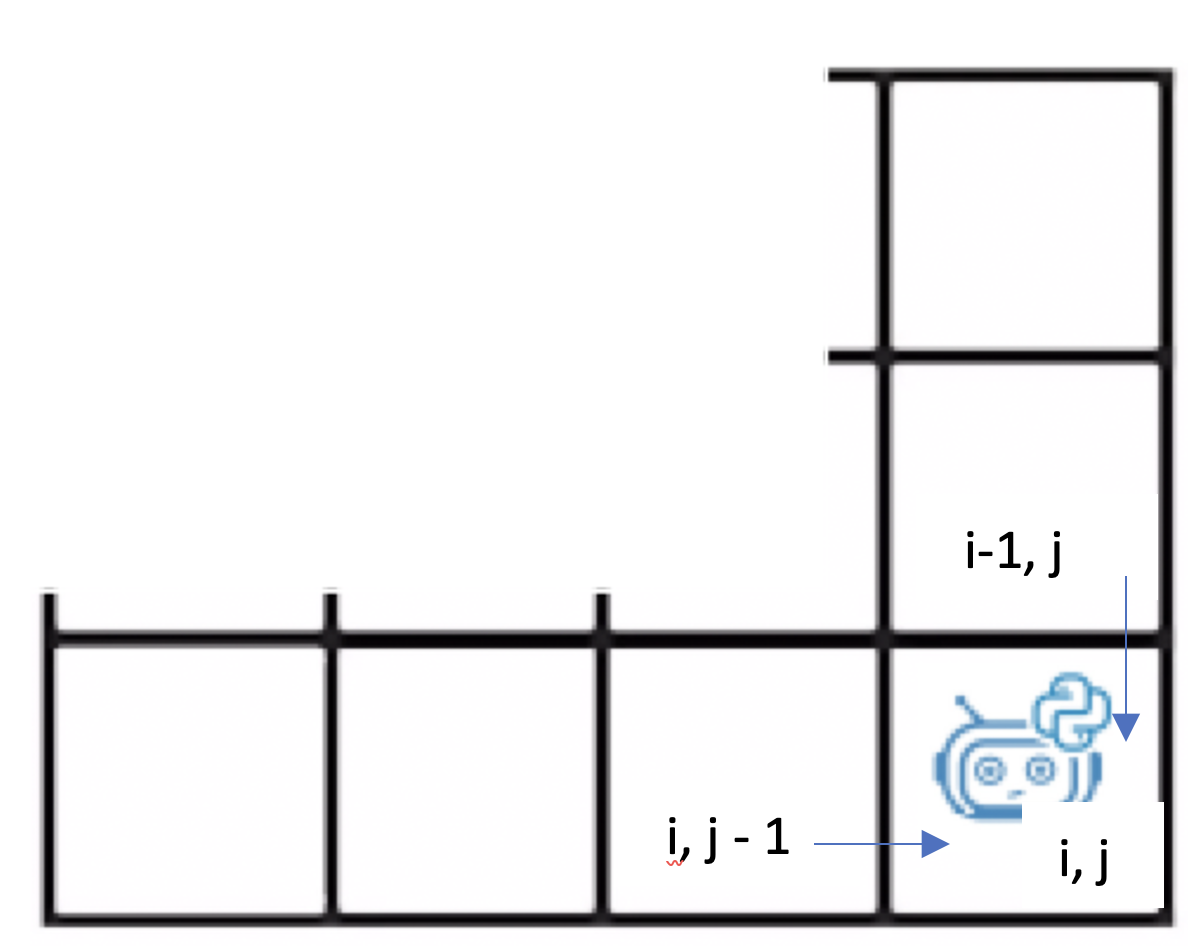
Если рассмотреть движение робота по сетке, то можно увидеть, что попасть в клетку с координатой
(i, j) можно лишь двумя способами: из клетки с координатой
(i, j-1), двигаясь из нее вправо и из клетки с координатой
(i-1, j), двигаясь из нее вниз.
Получается наша рекуррентная формула имеет вид:
ai,j = ai,j-1 + ai-1,j
4) Ограничения на формулу
Формула работает для всех
i > 1, j > 1 (при нумерации столбцов и строк, начиная с 1)
.
5) Определим порядок обхода таблицы
NxM.
В данном случае порядок обхода можно выполнить следующим образом:
- заполнить сначала первую строку и первый столбец единицами;
- заполнить остальную таблицу, используя рекуррентную формулу.
6) Определим, где находится ответ.
Ответ будет находится в правой нижней клетке таблицы, то есть
an,n