Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
Например, из 3 элементов (a,b,c)(a,b,c) по 2 можно образовать следующие сочетания: ab,ac,bc.
Число всех возможных сочетаний, которые можно образовать из n элементов по k, обозначается символом
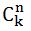
и вычисляется по формуле:
Есть два способа найти количество сочетаний
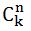
1. Найдем n!, k!, (n – k)! и по формуле приведенной сверху посчитаем количество, но из – за возможного переполнения этот способ можно использовать при n <= 12.
2. С помощью динамического программирования.
ДП будет выглядеть как треугольник Паскаля, на вершине и по краям стоят единицы, а каждое число равно сумме двух расположенных над ним чисел.
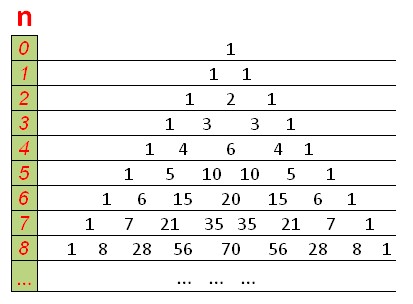
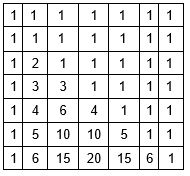
Функция считающая количество сочетаний с помощью динамическое программирование за О(n ^2 ):
int C(int n, int k)
{
vector<vector<int> > dp(n + 1, vector<int>(n + 1, 1)); // Создаем массив dp размером (n + 1, n + 1)
for (int i = 0; i <= n; i++) // Заполняем i-ю строку массива
{
for (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //пересчет (i;j) позиции через (i - 1; j - 1) и (i - 1; j)
}
}
return dp[n][k]; //вернем значение
}