Вместо того, чтобы просто посчитать хэш последовательности, мы можем запоминать значение на каждом из ее префиксов. Заметим, что это будут значения хэшей для последовательностей, равных соответствующему префиксу.
Имея такую структуру, можно быстро вычислять значение хэша для любого подотрезка этой последовательности (по аналогии с префиксными суммами).
Если мы хотим посчитать хэш подотрезка [l;r], то нужно взять хэш на префиксе r и вычесть хэш на префиксе l-1, домноженный на p в степени r-l+1. Почему это так, становится понятным, если расписать значения на префиксах и посмотреть, что происходит. Надеюсь у вас получится, глядя на эту картинку.
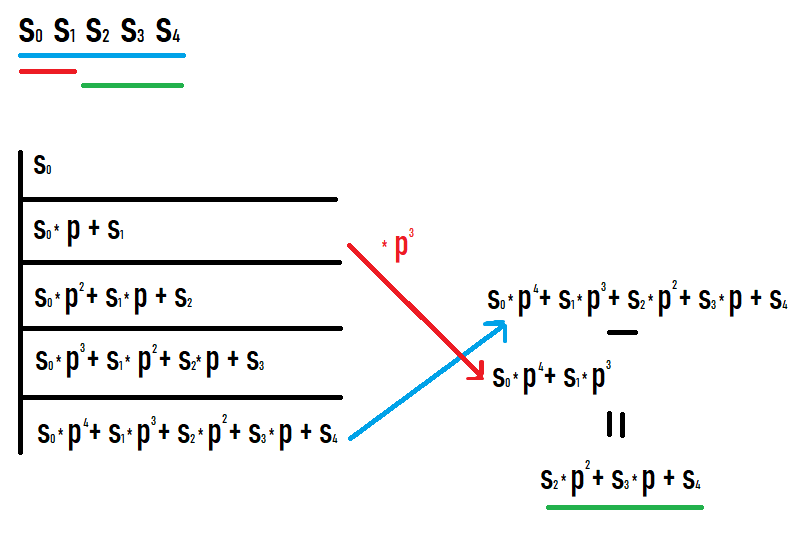
В результате таких действий мы получаем хэш подотрезка исходной последовательности. При этом этот хэш равен тому, если бы его считали как хэш от последовательности равной этому подотрезку (не требуется никаких дополнительных приведений степеней или т.п. для сравнения с другими значениями).
Тут есть два момента, которые стоит уточнить:
1) Чтобы быстро домножать на p в степени r-l+1, необходимо заранее предпосчитать все возможные степени p по модулю mod.
2) Необходимо помнить, что все вычисления мы производим по модулю mod, а поэтому может получиться так, что после вычитания префиксных хэшей мы получим отрицательное число. Чтобы этого избежать можно всегда прибавлять mod перед вычитанием. Также не забываем после домножений и всех сложений также брать значение по модулю.
В коде это выглядит так:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 1000003;
// основание и модуль хэширования
ll p, mod;
// префиксный хэш и степени p
ll h[MAXN], pows[MAXN];
// подсчет хэша подотрезка [l;r]
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int main()
{
// каким то способом получаем p и mod
// предпосчитываем степени p
pows[0] = 1;
for (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// основное решение задачи
//
return 0;
}