Рассмотрим этот алгоритм на примере поиска минимума (поиск максимума аналогичен).
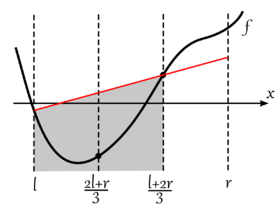
Пусть функция f(x)на отрезке [L,R] имеет минимум, и мы хотим найти точку xmin, в которой он достигается.
Так как в точке xmin минимум, то на отрезке [L,xmin] функция убывает, а на [xmin,R] — возрастает.
Для любых точек x′, x′′ ∈ [L,R] возможна одна из трех ситуаций:
- (A ) L < x′ < x′′< xmin и заничит f(L) > f(x′) > f(x′′) > f(xmin)
- (B) xmin<x′<x′′<r и значит f(xmin) < f(x′) < f(x′′) < f(R)
- (C) L< x′<= xmin <=x′′< R и значит f(L) > f(x′) и f(x′′) < f(R)
Разделим отрезок на три части определив точки L<a<b<R (например:
a=L+(R−L)/3 и
b=L+2(R−L)/3 ) и
посчитаем значения функции в точках
a и
b. Будут возможны два случая:
- f(a) > f(b) и тогда для точек a, b, xmin возможен случай (A) или (C) и => xmin ∈ [a,R];
- f(a) <= f(b) и тогда для точек a, b, xmin возможен случай (B) или (C) и => xmin ∈ [L,b];
Таким образом на каждом шаге отрезок поиска будет сокращается (на треть) и в итоге можно получить требуемое значение с заданной точностью.