скачать
SPARSE TABLE (разреженная таблица)
Sparse Table – структура данных, которая позволяет отвечать на запросы типа “найдите значение функции на неизменяемом массиве на отрезке [L;R]” и при этом занимает О(1) времени и О(n*logn) памяти, где n – размер массива.
Sparse Table (далее ST) корректно работает только с идемпотентными функциями*
Описание структуры:
Перед рассмотрением самого ST рассмотрим некоторый факт, на основе которого заключается весь смысл ST.
“Отрезок любой длины можно покрыть двумя отрезками, длины которых являются степенями двойки и при этом не превосходят длины отрезка, который необходимо покрыть” (можете доказать это сами или просто поверьте, что это правда).
Примеры:

В чем идея ST: давайте предподсчитаем нужную функцию в массиве на всех подотрезках, длины которых являются степенями двойки и далее будем пользоваться ими, чтобы отвечать на запросы.
Можно заметить, что некоторые подотрезки перекрываются дважды. Именно поэтому ST работает только с идемпотентными функциями.
Построение ST:
Пусть F() – функция, которую мы считаем на нужном массиве.
Заведем массив d[logn][n], где n – размер массива.
d[i][j] – F() на подотрезке исходного массива, длина которого 2^i и начало в j.
Очевидно, что мы знаем F() для подотрезков длины 2^0 т.е. 1 – это сами значения массива.
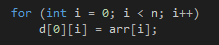
Далее будем подсчитывать значения следующим образом:
Пусть мы сейчас хотим узнать F() для длины 2^i. Мы уже посчитали значения для подотрезков длины 2^(i-1), а 2^i = 2 * 2^(i – 1), поэтому нам достаточно взять F() уже посчитанных значений двух подряд идущих подотрезков длины 2^(i-1) и начинающихся с текущей позиции.
Например:
Сейчас мы подсчитываем F() на подотрезке длины 2 и начинающегося с позиции 0. Мы уже знаем все значения на всех подотрезках длины 1. Поэтому нам достаточно взять F() с подотрезка длины 1 и начинающегося в позиции 0 и подотрезка длины 1 и начинающегося в позиции 1. Это и будет F() пары, начинающейся в позиции 0. То есть для каждой пары мы считаем через два подряд идущих единичных элемента, для каждой четверки через две подряд идущие пары и т.д.
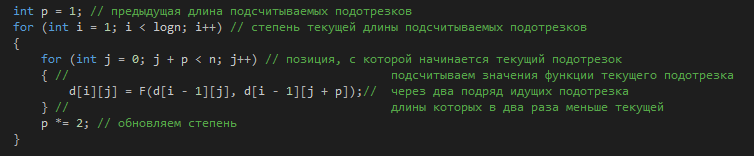
Асимптотика построения – О(n*logn).
Ответ на запрос:
Пусть нам пришел запрос на отрезок [L;R]. Первый вопрос, который приходит в голову: отрезками какой длины нужно перекрывать текущий? Нам необходимо вычислить такое, число, что оно является максимальной степенью двойки и при этом не превосходит длину отрезка-запроса. Чтобы не тратить лишнее время на вычисление этой величины, предподсчитаем эти значения до ответов на запросы.
Сделаем массив pows[MAX_LEN], где MAX_LEN – максимальная длина возможного отрезка-запроса.
pows[i] – такое число, что
2^pows[i] <= i < 2^(pows[i] + 1).
То есть для каждого числа (фактически для любой возможной длины отрезка-запроса) посчитаем максимальную степень двойки, что 2 в этой степени не больше текущего числа.
Подсчет массива pows:
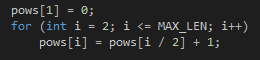
У нас есть необходимая длина, ее степень, подсчитанное значение функций на массиве для всех подотрезков всех степеней. Далее все относительно понятно: возьмем посчитанное значение с подотрезка определенной длины, который начинается в L(левой границе отрезка-запроса), значение с подотрезка определенной длины, который заканчивается в R(правой границе отрезка-запроса) и возьмем от них F(). Это и будет ответ. Так как, мы используем ST только для идемпотентных операций, то двойные перекрытия некоторых фрагментов нам не страшны.

*Об идемпотентных операциях:
Идемпотентность — свойство объекта или операции при повторном применении операции к объекту давать тот же результат, что и при одинарном.
Формально, функция F является идемпотентной, если выполняется F(x;x) = x;
Min(5, 5) = 5 -> min – идемпотентная функция
Sum(5; 5) = 10 -> сумма не идемпотентная функция
Часто используемые в задачах идемпотентные операции: min, max, gcd (НОД).