C++. Быстрая сортировка


Быстрая сортировка

Быстрая сортировка, сортировка Хоара (англ. quicksort), часто называемая qsort (по имени в стандартной библиотеке языка Си) — алгоритм сортировки, разработанный английским информатиком Чарльзом Хоаром во время его работы в МГУ в 1960 году.

Один из самых быстрых известных универсальных алгоритмов сортировки массивов: в среднем \(O(n\log n)\) обменов при упорядочении n элементов; из-за наличия ряда недостатков на практике обычно используется с некоторыми доработками.

Быстрый метод сортировки функционирует по принципу "разделяй и властвуй" (рекурсивное разбиение решаемой задачи на две или более подзадачи того же типа, но меньшего размера, и комбинирование их решений для получения ответа к исходной задаче).

QuickSort является существенно улучшенным вариантом алгоритма сортировки с помощью прямого обмена (например, рассмотренной нами "Пузырьковой сортировки"), известного в том числе своей низкой эффективностью. Принципиальное отличие состоит в том, что в первую очередь производятся перестановки на наибольшем возможном расстоянии и после каждого прохода элементы делятся на две независимые группы. (Таким образом улучшение самого неэффективного прямого метода сортировки дало в результате один из наиболее эффективных улучшенных методов.)

Преимущества QuickSort по сравнению с другими алгоритмами быстрой сортировки заключается в том, что он не использует дополнительных массивов, сортировка происходит "на месте".

Алгоритм состоит из трёх шагов:

  1. Выбор опорного элемента из массива (X).
  2. Этап разделения. Перераспределение элементов в массиве таким образом, что элементы меньше опорного помещаются перед ним, а больше или равные - после. 
    A[i] < X
    		 
    A[i]>=X
    Теперь элементы расположены так, что ни один элемент из первой группы при сортировке не окажется во второй группе, и наоборот.
    Поэтому достаточно отсортировать отдельно каждую часть массива - это и есть подход "разделяй и властвуй".
  3. Рекурсивное применение первых двух шагов к двум подмассивам слева и справа от опорного элемента. Рекурсия не применяется к массиву, в котором только один или отсутствуют элементы.
Процедура сортировки должна принимать три параметра:
- массив, который сортируем;
- индекс первого элемента сортируемого участка;
- индекс последнего элемента сортируемого участка.
 
Алгоритм на псевдокоде:
АЛГ QUICKSORT(A[], START, END)
   // если условие выполняется, то в рабочей части массива 
   // меньше двух элементов,   
   // то есть сортировать уже ничего не нужно
   ЕСЛИ START >= END, ТО ВЫЙТИ ИЗ ПРОЦЕДУРЫ   
   
   // в качестве опорного элемента можно брать 
   // случайное число на отрезке сортируемого участка, 
   // можно брать средний элемент 
   X = СЛУЧАЙНЫЙ ЭЛЕМЕНТ МАССИВА НА ОТРЕЗКЕ [START; END]  
   
   L = START, R = END
   ПОКА L <= R
       // ищем элементы для перестановки
       ПОКА A[L] < X
           L += 1
       ПОКА A[R] > X
           R -= 1
       // если нужно делаем перестановку
       ЕСЛИ L <= R, то
           МЕНЯЕМ МЕСТАМИ A[L] И A[R]
           L += 1
           R -= 1

    // осталось отсортировать отдельно первую и вторую части 
    QUICKSORT(A, START, R)
    QUICKSORT(A, L, END)
Данная процедура может отсортировать любую часть массива, для этого достаточно верно указать параметры START и END.

Сравнение времени работы (в секундах) различных алгоритмов сортировки для массивов разного размера (N):
N Пузырьковая сортировка Сортировка вставками Быстрая сортировка
5000 0,039 0,016 0,00031
15000 0,359 0,141 0,00078
50000 3,985 1,469 0,00297

Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, быстрая сортировка в худшем случае будет выполняться O(n²).

Задача для тренировки:

Быстрая сортировка: Начало (С++)

Сортировка слиянием
Алгоритм был изобретён Джоном фон Нейманом в 1945 году.
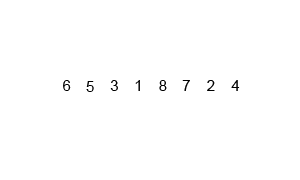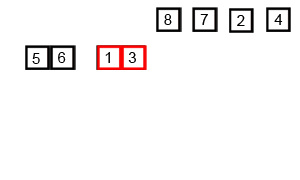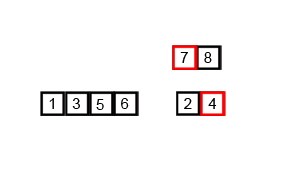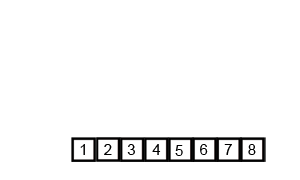Идея сортировки
1) Возьмем массив. Если он состоит из одного элемента, то он уже отсортирован
2) Если элементов больше, чем один, то разобьем массив на две равные части (с точностью до единицы) и отсортируем каждую часть, применив рекурсивно тот же алгоритм. 
3) Далее, "сольем" все отсортированные части в один массив.
 
Как "слить" все части в один массив?
  1. Будем хранить индексы начала двух отсортированных частей.
  2. Создадим новый список следующим образом:
    1. из двух элементов, на которые указывают индексы, будем выбирать меньший и дописывать его в новый список;
    2. сдвинем индекс, элемент которого мы взяли, на следующий элемент списка;
    3. если закончились элементы в одной из сливаемых частей, то элементы второй мы просто добавим в конец итогового списка.
  3. Полученный отсортированный список необходимо поместить на место сливаемых частей.
 
Псевдокод алгоритма слияния
Функция сливает две части массива a - [left;mid) и [mid;right)
  
ФУНКЦИЯ merge(a, left, mid, right)    // a - массив, размерностью n; left, mid, right - целые числа, индексы элементов массива
    it1 = 0
    it2 = 0
    result: int[right - left]   // результирующий массив
  
    ПОКА left + it1 < mid И mid + it2 < right
        ЕСЛИ a[left + it1] < a[mid + it2]
            result[it1 + it2] = a[left + it1]
            it1 += 1
        ИНАЧЕ
            result[it1 + it2] = a[mid + it2]
            it2 += 1
  
    ПОКА left + it1 < mid
        result[it1 + it2] = a[left + it1]
        it1 += 1
  
    ПОКА mid + it2 < right
        result[it1 + it2] = a[mid + it2]
        it2 += 1
  
    ДЛЯ i ОТ 0 ДО it1 + it2
        a[left + i] = result[i]

    ВЕРНУТЬ a
 
 
Рекурсивный алгоритм сортировки слиянием
Функция сортирует подотрезок массива a с индексами в полуинтервале  [left; right)
  
ФУНКЦИЯ mergeSortRecursive(a, left, right)    // a - массив, left, right - индексы полуинтервала сортировки
    if left + 1 >= right
        ВЕРНУТЬ a
    mid = (left + right) / 2
    mergeSortRecursive(a, left, mid)
    mergeSortRecursive(a, mid, right)
    merge(a, left, mid, right)
    ВЕРНУТЬ a
 
Итеративный алгоритм сортировки слиянием
При итеративном алгоритме используется на O(logn) меньше памяти, которая раньше тратилась на рекурсивные вызовы. 
ФУНКЦИЯ mergeSortIterative(a, n) // a - массив; n - длина массива
    ДЛЯ i ОТ 1 ДО n, ШАГ i *= 2
        ДЛЯ j ОТ 0 ДО n - i, ШАГ j += 2 * i
            merge(a, j, j + i, min(j + 2 * i, n))
    ВЕРНУТЬ a
 
Время работы
Для оценки времени работы, составим рекуррентное соотношение.
Пусть T(n) - время сортировки массива длины n, тогда для сортировки слиянием справедливо:
T(n) = 2T(n/2)+O(n)
O(n) - время, необходимое на то, чтобы слить два массива длины n.
Распишем это соотношение:
T(n) = 2T(n/2) + О(n) = 4T(n/4) + 2O(n) = ... = T(1) + log(n)O(n) = O(nlog(n)).
 
Сложность алгоритма O(nlog(n))
 
Дополнительные материалы
1) Сортировка слиянием. Вики-конспекты ИТМО.

Задача для тренировки:

Сортировка слиянием

Пропустить Навигационные Ссылки.
Чтобы оставить комментарий нужна авторизация