Графы. Основные понятия
Граф - это абстрактная структура данных, состоящая из набора вершин (узлов), связанных ребрами (дугами).
Графы широко применяются для моделирования и анализа различных ситуаций и взаимосвязей. Использование графов позволяет упростить решение многих задач и повысить эффективность работы в различных областях, таких как: транспортная система, социальные связи, компьютерные сети, биоинформатика, геоинформационные системы, управление проектами и др.
Основные характеристики графов
Граф может быть
неориентированным, что означает отсутствие различия между двумя вершинами, связанными с каждым ребром; или его ребра могут быть направлены от одной вершины к другой - в таком случае мы будем говорить об
ориентированном графе.
| Неориентированный граф |
Ориентированный граф |
.png) |
.png) |
Если ребрам графа присваивается некоторое значение, то такой граф называется взвешенным. Если веса всех ребер одинаковы, то граф называется невзвешенным графом.
| Взвешенный граф |
.png) |
Еще несколько определений
Если ребро соединяет две вершины, то оно инцидентно этим вершинам, а вершины, связанные ребром инцендентными ребру. Вершины, связанные ребром называются смежными.
Ребра называются кратными, если они соединяют одну и ту же пару вершин. Ребро называется петлей, если его концы совпадают.
В различных задачах кратные ребра и петли могут не играть существенной роли, поэтому во многих случаях рассматриваются простые графы, которые лишены петель и кратных ребер. Простые графы обладают изящной и простой структурой, что делает их особенно привлекательными для анализа и решения задач.
Структура данных граф (V,E) состоит из:
- Коллекции вершин (
V - vertex) или узлов (nodes).
- Коллекции ребер (
E - edges) или путей.
Как описать структуру данных граф?
Наиболее часто используют следующие два способа представления (описания) графа:
1. Матрица смежности - это квадратная матрица, где строки и столбцы соответствуют вершинам графа. Значение в ячейке (i, j) равно 1, если между вершинами i и j существует ребро, и 0, если ребра нет. Для простого графа без петель и кратных ребер матрица смежности будет симметричной относительно главной диагонали. Этот подход обеспечивает компактное представление графа в виде матрицы и позволяет быстро определить наличие ребра между двумя вершинами.
Матрицы смежности
для неориентированного графа |
Матрицы смежности
для ориентированного графа |
.png) 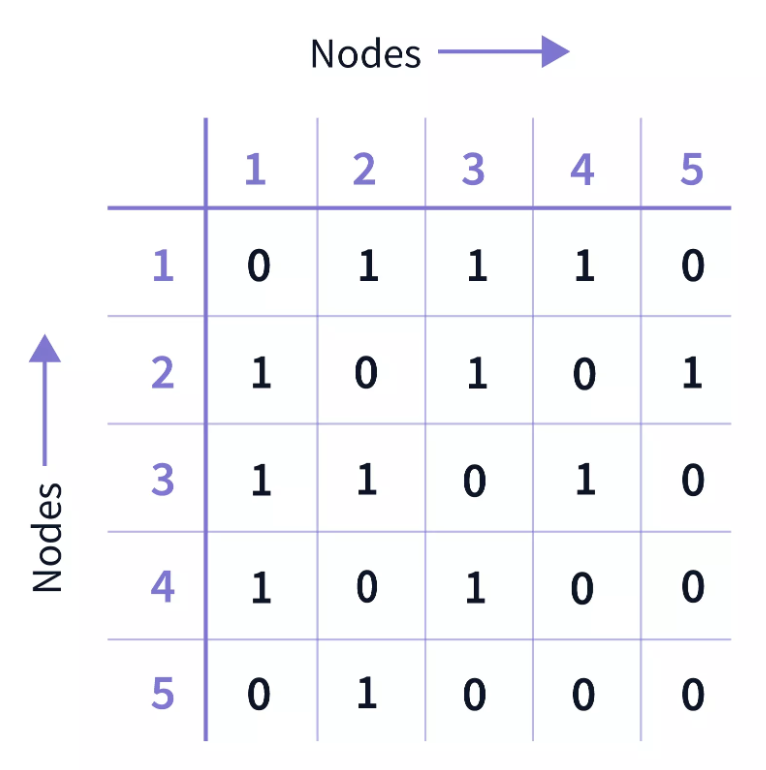 |
.png) 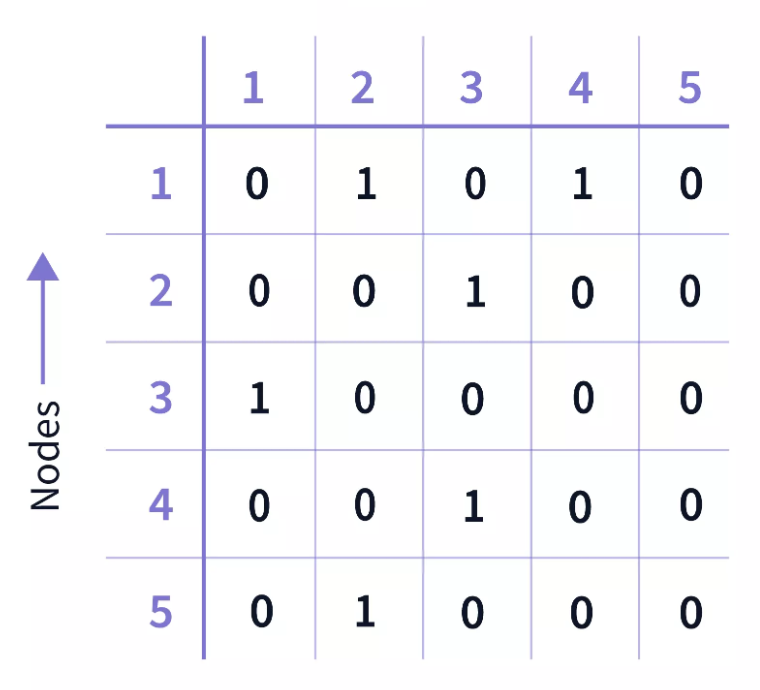 |
2. Список смежности (список вершин). Представление графа в виде списка смежности основано на перечислении каждой вершины графа и указании соседних вершин, с которыми она связана. Для каждой вершины создается список ее соседей. Этот подход позволяет более эффективно использовать память, особенно для разреженных графов, так как он не требует выделения памяти для всей матрицы смежности. Кроме того, список вершин обеспечивает легкость добавления и удаления ребер в графе.
Список вершин
для неориентированного графа |
Список вершин
для ориентированного графа |
.png) |
1: {2, 3, 4}
2: {1, 3, 5}
3: {1, 2, 4}
4: {1, 3}
5: {2} |
.png) |
1: {2, 4}
2: {3}
3: {1}
4: {3}
5: {2} |
Оба этих способа представления графа имеют свои преимущества и могут быть выбраны в зависимости от конкретной задачи и требований. Матрица смежности удобна для быстрого доступа к информации о связях между вершинами, а список вершин позволяет более гибко управлять структурой графа.
3. Список ребер. Список ребер позволяет легко и быстро получить информацию о каждом ребре и его свойствах, таких как вес или направление в ориентированном графе. Это может быть полезно, например, при решении задач на поиск кратчайшего пути в графе или при обнаружении циклов.
В неориентированном графе каждое ребро указывается только один раз, например, если есть ребро (1, 2), то нет необходимости добавлять и ребро (2, 1) в список ребер.
В ориентированных графах порядок чисел в паре, представляющей ребро, определяет направление ребра. Первое число указывает на начальную вершину, откуда ребро исходит, а второе число указывает на конечную вершину, куда ребро направлено.
Список ребер
для неориентированного графа |
Список ребер
для ориентированного графа |
.png) |
[
(1, 2),
(1, 3),
(1, 4),
(2, 3),
(2, 5),
(3, 4)
] |
.png) |
[
(1, 2),
(1, 4),
(2, 3),
(3, 1),
(4, 3),
(5, 2)
] |
Если граф имеет большое количество вершин и ребер, то список ребер может занимать много памяти и стать неэффективным для поиска конкретной вершины или ее смежных вершин.