Рекурсия
Процедура или функция может содержать внутри себя вызов другой процедуры. В том числе, подпрограмма может вызывать саму себя. В этом случае компьютеру все равно. Он также как и всегда последовательно сверху вниз выполняет те команды, которые ему встретились.
Если вспомнить математику, то там можно встретить принцип математической индукции. Он заключается в следующем:
некоторое утверждение справедливо для всякого натурального n, если
1. оно справедливо для n = 1 и
2. из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k + 1.
В программировании этот прием называют рекурсией.
Рекурсия - это способ определения множества объектов через само это множество на основе заданных простых базовых случаев.
Рекурсивной же будет называться процедура (функция), которая вызывает саму себя напрямую или через другие процедуры и функции.
Пример
def Rec(a):
if (a>0): Rec(a-1)
print(a)
Схематично работу рекурсии можно изобразить блок-схемой
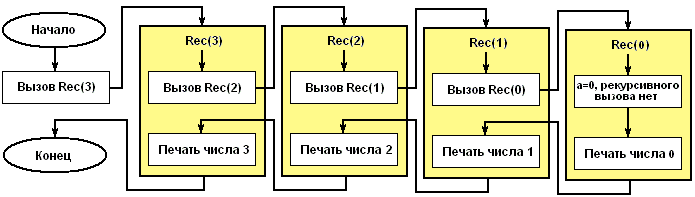
Процедура Rec() выполняется с параметром 3. Затем внутри процедуры с параметром 3 вызывается процедура с параметром 2 и т.д., пока не произойдет вызов процедуры с параметром 0. При вызове процедуры с параметром 0 рекурсивного вызова уже не произойдет и процедуры с параметром 0 напечатает число 0 и закончит работу. Затем управление передается обратно в процедуру с параметром 1, она также заканчивает свою работу печатает число 1 и т.д. до процедуры с параметром 3.
Все вызвавшиеся процедуры хранятся в памяти, до тех пор пока не закончат свою работу. Количество одновременно работающих процедур называется глубиной рекурсии.
|
Рекурсия как замена цикла
Мы увидели, что рекурсия - это повторное выполнение содержащихся команд в подпрограмме. А это в свою очередь аналогично работе цикла. Существуют языки программирования, в которых конструкция цикла отсутствует вовсе. Например, Пролог.
Попробуем сымитировать работу цикла for.
Цикл for содержит переменную-счетчик шагов. В рекурсивной подпрограмме такую переменную можно передавать в качестве параметра.
# Процедура LoopImitation() с двумя параметрами
# Первый параметр – счетчик шагов,
# второй параметр – общее количество шагов
def LoopImitation(i, n):
print("Hello N", i) # Оператор, который необходимо выполнять (повторять)
# при любом значении i
if i < n: # Пока счетчик цикла не станет равным значению n,
LoopImitation(i + 1, n) # вызываем еще раз эту же процедуру,
# с параметром i+1 (переход к следующему значению i)
|
Рекурсия и итерации
Чтобы понять рекурсию, надо понять рекурсию...
Итерация в программировании - один шаг циклического процесса обработки данных.
Часто итерационные алгоритмы на текущем шаге (итерации) используют вычисленный на предыдущих шагах результат такой же операции или действия. Одним из примеров таких вычислений служат вычисления рекуррентных соотношений.
Простым примером величины, вычисляемой с помощью рекуррентных соотношений, является факториал: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
Вычисление значения на каждом шаге (итерация) это \(N=N \cdot i\) . При вычислении значения \(N\), мы берем уже сохраненное значение \(N\).
Факториал числа можно также описать с помощью рекуррентной формулы:
\(\begin{equation*} n! = \begin{cases} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{cases} \end{equation*}\)
Можно заметить, что это описание является ни чем иным как рекурсивной функцией.
Здесь первая строка ( \(n <= 1\)) - это базовый случай (условие окончания рекурсии), а вторая строка - переход к следующему шагу.
| Рекурсивная функция вычисления факториала |
Итерационный алгоритм |
def Factorial(n):
if n > 1:
return n * Factorial(n - 1)
else:
return 1
|
x = 1
for i in range(1, n + 1):
x = x * i;
|
Следует понимать, что вызов функций влечет за собой некоторые дополнительные накладные расходы, поэтому не рекурсивный вариант вычисления факториала будет несколько более быстрым.
Вывод: там, где можно написать программу простым итерационным алгоритмом, без рекурсии, то надо писать без рекурсии. Но все таки существует большой класс задач где вычислительный процесс реализуется только рекурсией.
С другой стороны - рекурсивные алгоритмы чаще всего более понятны.
|
Задача
В алфавите языка племени «Тумба-Юмба» четыре буквы: «K», «L», «M» и «N». Нужно вывести на экран все слова, состоящие из n букв, которые можно построить из букв этого алфавита
Задача представляет собой обычную задачу на перебор, которую можно свести к задаче меньшего размера.
Будем последовательно подставлять буквы к слову.
На первой позиции слова может стоять одна из 4-х букв алфавита ( K, L, M, N).
Сначала первой поставим букву ' K'. Тогда для того, чтобы получить все варианты с первой буквой ' K', нужно перебрать все возможные комбинации букв на оставшихся n-1 позициях и .т.д. (см. рисунок)
Таким образом, мы вышли на рекурсивное решение: в цикле перебрать все возможные первые буквы (ставя по очереди каждую букву алфавита на первое место) и для каждого случая построить все возможные "хвосты" длиной n-1.
Рекурсивный перебор символов
Остановить рекурсию и вывести готовое слово нужно тогда, когда оставшаяся часть пустая ( n = 0), т.е. все буквы уже выбраны.
Рекурсивная процедура будет выглядеть следующим образом:
def TumbaWords(word, alphabet, n):
if n < 1:
print(word)
return
for c in alphabet:
TumbaWords(word+c, alphabet, n - 1)
|
