TUZ_2-04 Поиск решения обратной гипотезы Коллатца
2.4. Поиск решения обратной гипотезы Коллатца
Гипотеза Коллатца – это математическое утверждение, согласно которому любое целое число меньше 2
68, удовлетворяющее двум условиям, указанным в формуле 2.2, в конечном итоге достигнет числа 1 после конечного числа шагов.
Гипотеза касается последовательностей и может быть выражена следующим образом:
- берется натуральное число n, и из него генерируются два числа в соответствии с формулой 2.2.
- Этот процесс повторяется для всех последующих чисел, пока последовательность не закончится единицей.
Ваша задача: написать функцию, которая вычисляет решение обратной гипотезы Коллатца.
Если вычисление дает неверный результат (т. е. нецелое число), то функция должна вернуть значение None.
Обратная гипотеза Коллатца удваивает четные числа, а из нечетных чисел вычитает 1 и делит разность на 3. Формально гипотеза Коллатца представлена в формуле 2.2, а обратная гипотеза Коллатца – в формуле 2.3.
В табл. 2.4 оказаны ожидаемые результаты для некоторых входных данных.
| Таблица 2.4. Некоторые ожидаемые результаты для разных входных значений в обратной гипотезе Коллатца |
| shape |
Ожидаемый результат |
| dd |
4 |
| uudduuudd |
None |
| ududududddddudddd |
15 |
| uduuddduddduu |
None |
Например, если входная строка shape = ududddd, то на первом этапе выбирается последний элемент в shape – символ d и применяется соответствующий ему первый случай в формуле 2.3, т. е. выполняется умножение на 2, в результате получается x = x × 2 (первоначально x = 1). Далее, продолжая просматривать shape с конца, обнаруживаем три следующих подряд символа d, поэтому x обновляется следующим образом: x = 2 → 2 × 2 = 4, x = 4 → 4 × 2 = 8, x = 8 → 8 × 2 = 16. На следующем шаге обнаруживается символ u, поэтому применяется второй случай в формуле 2.3 и из числа x вычитается 1, а полученная разность делится на 3, соответственно, x = 16 → (16–1)/3 = 5, далее снова следует символ d, поэтому x = 5 → 5 × 2 = 10. Последним следует символ u, соответственно, x = 10 → (10 × 1)/3 = 3. То есть решением обратной гипотезы Коллатца для shape = ududdddd является число 3. Чтобы проверить правильность полученного значения, строку, что была передана в обратную гипотезу Коллатца, нужно сравнить со строкой, получаемой в ходе решения прямой гипотезы Коллатца, согласно формуле 2.2, которая применяется, пока x не достигнет 1. Итак, возьмем предыдущий полученный результат x = 3 и пустую строку t. На первом шаге имеем: num = x, (num mod 2) = 1, поэтому num = (3 ∗ num + 1) → num = (3 ∗ 3 + 1) = 10 и t = u. Продолжим, num = 10, 10 mod 2 = 0, поэтому 10/2 = 5 и t = ud. На следующем шаге num = 5, и мы все еще не достигли единицы, поэтому num = 5 ∗ 3 + 1 = 16 и t = udu. Далее выполняется такая последовательность шагов:
num = 16 mod 2 = 0 → num = num/2 = 8 → t = udud,
num = 8 mod 2 = 0 → num = num/2 = 4 → t = ududd,
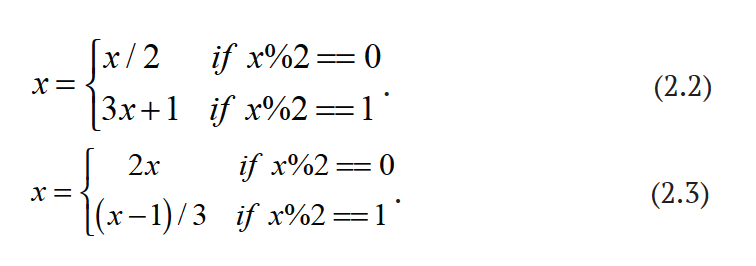
num = 4 mod 2 = 0 → num = num/2 = 2 → t = ududdd,
num = 2 mod 2 = 0 → num = num/2 = 1 → t = ududddd.