Ускоряем рекурсию
Когда мы используем рекурсию для вычисления значений функции, иногда мы можем столкнуться с ситуацией, когда одни и те же значения вычисляются несколько раз.
Возьмем рекуррентное соотношние для вычисления чисел Фибоначчи: F(n) = F(n-1) + F(n-2)
На рисунке ниже изображено дерево, которое показывает какие значения вычисляются для того, чтобы вычислить шестое число Фибоначчи.
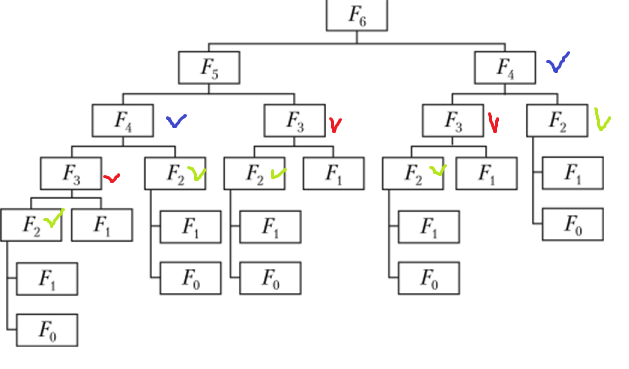
Как каждый раз, когда функция вызывается, она начинает вычисления сначала, не имея доступа к результатам предыдущих вычислений. В результате функция может многократно вычислять значения для одних и тех же значениях параметра (на рисунке такие значения отмечены одним и тем же цветом). Это приводит к избыточным вычислениям и замедлению работы программы.
В рамках решения задач ЕГЭ в таких случаях можно использовать метод динамического программирования одним из двух способов.
1) Использовать мемоизацию. Это означает сохранение уже вычисленных значений в памяти и их повторное использование при последующих вызовах функции с теми же аргументами.
Для этого можно использовать словарь или список. Кроме этого, в Python есть специальный декоратор @lru_cache() модуля functools, который запоминает возвращаемый функцией результат и использует его при повторных вызовах. Декоратор пишется непосредственно перед описанием функции.
2) Использовать итеративный подход. То есть уйти от реализации функции и написать вычисления всех значений по шагам с использованием цикла. При этом также запоминая вычисленные значения, например в списке, и использовать их при вычислении следующих значений.
Первый способ достаточно прост, достаточно перед описанием функции подписать декоратор. Но своить второй способ также необходимо, в связи с тем, что глубина рекурсии ограничена размером стека и при больших значениях параметра отведенного размера стека может не хватить.
Пример 2. Запоминаем вычисленные значения, используя декоратор
Алгоритм вычисления функции F(n) задан следующими соотношениями:
F(n) = n при n ≤ 3
F(n) = F(n–3) + F(n/3) + n, если n > 3 и кратно трём,
F(n) = F(n–1) + F(n–2) + F(n-3), если n > 3 и не кратно трём.
Чему равно значение функции F(50) + F(65)?
Знак / обозначает операцию целочисленного деления.
В данном примере вычисление значения функции при
n не кратном трём будет очень много вычислений значений функции при одних и тех же значениях параметра
n. Это помешает нам вычислить ответ в приемлемое время. Поэтому здесь не обойтись без декоратора
@lru_cache, который позволит выполнить вычисления значительно быстрее.