2.7.1 Множества и логика. Множества

Множества

Множество — некоторый набор элементов, каждый из которых отличается от остальных. Множество может состоять из конечного числа элементов (например, множество букв русского алфавита), бесконечного числа элементов (например, множество натуральных чисел) или вообще быть пустым (например, множество слонов, живущих на Северном полюсе). Пустое множество обозначается символом ∅. Множества, с которыми работает компьютер, не могут быть бесконечными, потому что его память конечна.

Чтобы определить множество, мы можем перечислить все его элементы. Например, множество, состоящее из Васи, Пети и
Коли, можно записать так: {Вася, Петя, Коля}. 

Можно задать множество иначе: определить условие (логическое выражение), которое должно быть истинным для всех элементов множества и ложным для всех элементов, не входящих во множество. Например, можно ввести множество драконов с пятью зелёными хвостами или множество чисел, делящихся на 11.

Хотя множество — это математическое понятие, с множествами мы имеем дело каждый раз, когда обращаемся к поисковой
системе в Интернете: ведь нас интересует множество страниц, на которых есть нужная нам информация. Задать такое множество перечислением элементов невозможно: во-первых, мы не знаем адресов этих страниц; во-вторых, их очень много. Поэтому для того, чтобы задать нужное нам множество, требуется написать поисковый запрос — логическое выражение, которое его определяет.
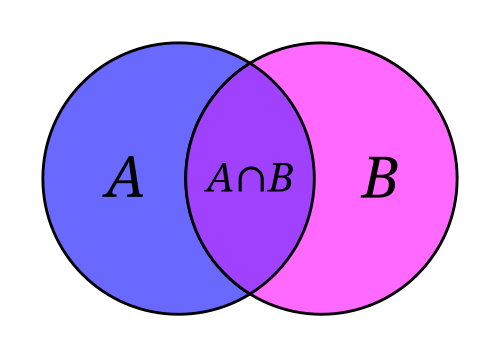
Пересече́ние мно́жеств  — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам. Пересечение двух множеств ${\displaystyle A}$ и ${\displaystyle B}$ обычно обозначается ${\displaystyle A\cap B}$.

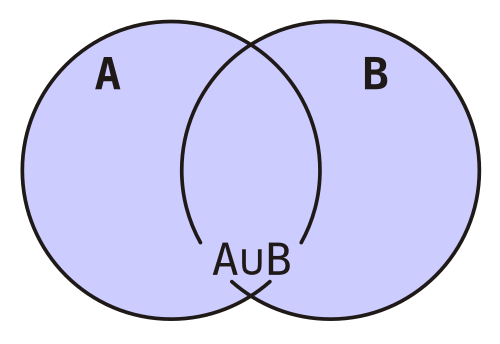
Объедине́ние мно́жеств (су́мма или соедине́ние)  — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств ${\displaystyle A}$ и ${\displaystyle B}$ обычно обозначается ${\displaystyle A}$ ∪ ${\displaystyle B}$, но иногда можно встретить запись в виде суммы ${\displaystyle A+B}$.

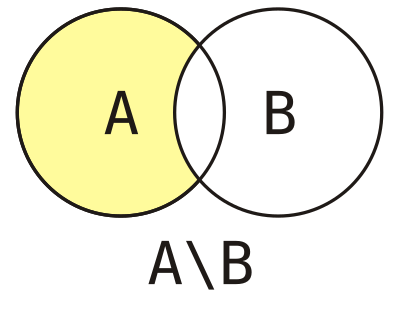
Ра́зность двух мно́жеств — операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств ${\displaystyle A}$ и ${\displaystyle B}$ обозначается как ${\displaystyle A\setminus B}$, но иногда можно встретить обозначение ${\displaystyle A-B}$ и ${\displaystyle A\sim B}$.

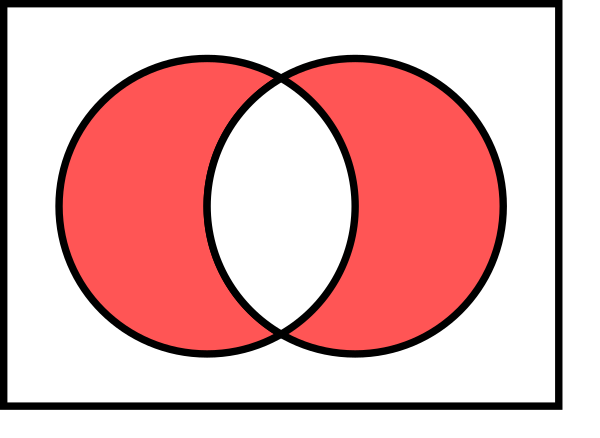
Симметри́ческая ра́зность двух множеств — операция, результатом которой является новое множество, включающее все элементы исходных множеств, не принадлежащие одновременно обоим исходным множествам. Другими словами, если есть два множества ${\displaystyle A}$ и ${\displaystyle B}$, их симметрическая разность есть объединение элементов ${\displaystyle A}$, не входящих в ${\displaystyle B}$, с элементами ${\displaystyle B}$, не входящими в ${\displaystyle A}$. На письме для обозначения симметрической разности множеств ${\displaystyle A}$ и ${\displaystyle B}$ используется обозначение ${\displaystyle A△B}$, реже используется обозначение ${\displaystyle A\dot{-}B}$${\displaystyle }$.