У Гудвина есть последовательность чисел из которой он хочет удалить три элемента так, чтобы последовательность была наиболее симпатичной.
Кривизна последовательности задается функцией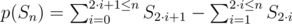 
, то есть разностью, между суммой элементов, стоящих на нечетных местах, и суммой элементов, стоящих на четных местах.
После удаления из последовательности трех элементов все остальные сдвигаются на нужные места. Например, из последовательности {1, 2, 3, 4, 5} можно получить последовательность {2, 4}.
Входные данные
В первой строке записано целое число n (4 ≤ n ≤ 106) — количество элементов в исходной последовательности. Во второй строке записаны n разделенных пробелами целых чисел — члены последовательности, разделенные пробелами. Все числа в последовательности по модулю не превышают 109.
Выходные данные
Выведите единственное число — минимальную кривизну последовательности, которая может быть получена из данной удалением трех элементов.
Примеры тестов
Входные данные
Входные данные
5
1 2 3 4 5
Примечание
Тесты разделены на группы, но оцениваются отдельно
- n ≤ 81 — 20 баллов
- n ≤ 300 — 10 баллов
- n ≤ 5000 — 20 баллов
- Без дополнительных ограничений — 50 баллов