| 3 |
5
0 0
0 4
4 0
1 1
1 2 |
96 |
Одна из перестановок, удовлетворяющих свойству - (0,0),(0,4),(4,0),(1,2),(1,1).
Для этой перстановки
- Сначала она рисует отрезки между каждой парой (0,0),(0,4), и (4,0).
- Затем она рисует отрезки от (0,0), (0,4), и (4,0) до (1,2).
- Наконец, она рисует отрезки от (1,2), (4,0), и (0,0) до (1,1).
Рисунок:
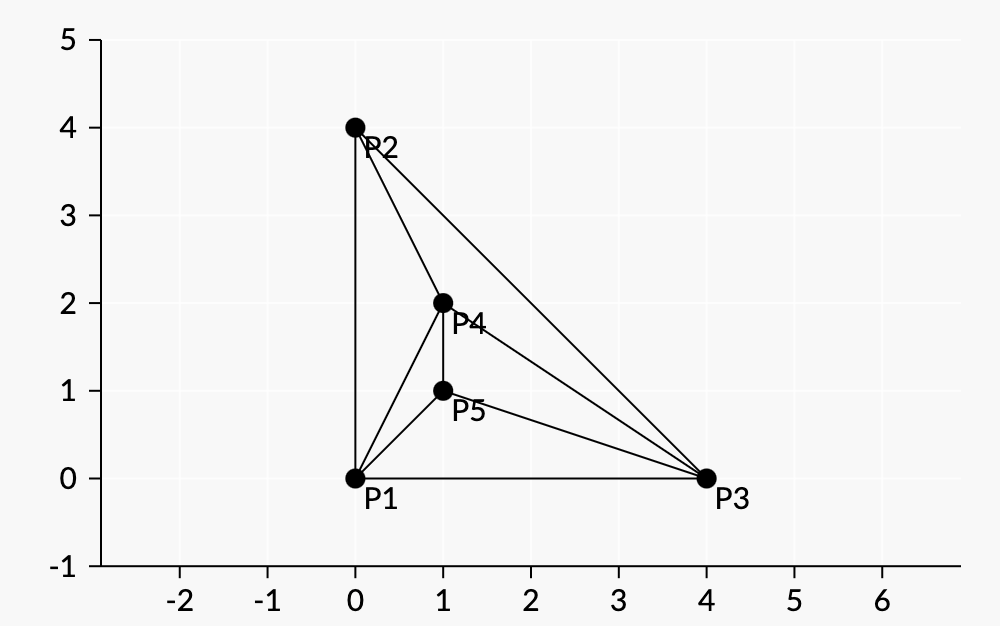
Перестановка не удовлетворяет свойству, если её первые четыре точки (0,0)(0,0), (1,1)(1,1), (1,2)(1,2), и (0,4)(0,4) в некотором порядке. |