Магическим квадратом называют таблицу, в которой записаны числа 123… по одному разу, так что сумма чисел в каждой строке и в каждом столбце равные. Мы расскажем вам об одном из методов построения магических квадратов (его называют сиамским). Он годится только для построения квадратов с нечетной стороной (3355…) .
Поставим число 1 в верхнюю клетку центрального столбца. Далее будем двигаться по диагонали вправо-вверх, расставляя в клетки последовательно числа 234… . Если мы вышли за пределы таблицы вверх, то нужно перейти к нижней клетке того же столбца и продолжить с нее. Если мы вышли за правую границу, нужно перейти к левой клетке той строки, куда мы должны были попасть. Если же мы одновременно вышли и вверх, и вправо, то нужно перейти в левую нижнюю клетку квадрата.
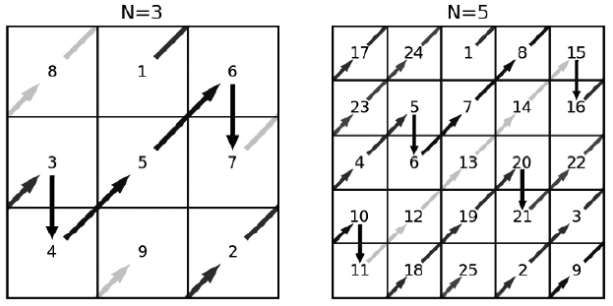
Если в следующей клетке на нашем пути уже стоит число, то вместо хода “вправо-вверх” нужно сделать ход “вниз” (опять же, если мы при этом выйдем за границы квадрата, нужно перейти к верхней клетке того же столбца). Примеры для квадратов 33 и 55 показаны на рисунках.
 Входные данные
Входные данные
На вход подается одно натуральное нечетное число N, не превосходящее 30 – размер квадрата.
Выходные данные
Выведите числа, записанные в квадрате. Выравнивать числа по столбцам не обязательно. Обратите внимание: требуется вывести именно магический квадрат, полученный применением указанного метода.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
8 1 6
3 5 7
4 9 2 |
| 2 |
5 |
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9 |