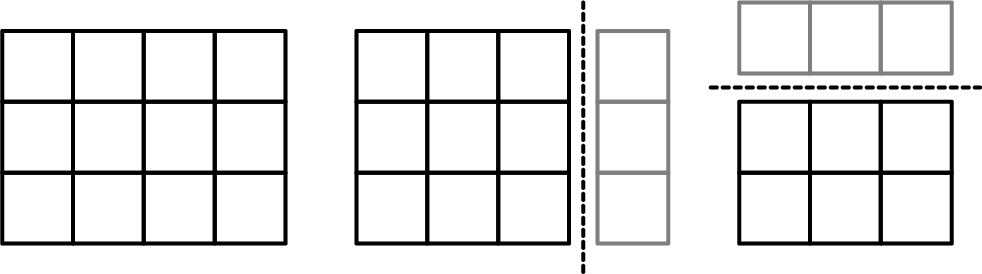Сегодня у Кроша день рождения! По этому поводу он испек огромный торт. Торт представляет собой прямоугольник n × m , разделенный на nm единичных квадратиков горизонтальными и вертикальными линиями из крема.
На праздник в гости к Крошу пришли Совунья и Нюша. По законам гостеприимства, Крош должен поделиться с своим тортом. Для этого он хочет по очереди отрезать от торта два куска и раздать их гостьям.
Отрезать кусок от торта Крош может так: разделить торт на два прямоугольника одним разрезом, проходящим по одной из горизонтальных или вертикальных линий (таким образом, после разреза оба прямоугольника имеют целые длины сторон). Далее, Крош выбирает один из этих прямоугольников и отдает очередной гостье.
После того, как Крош два раза отрежет кусок от своего торта, оставшуюся часть он съедает сам. Сегодня торт получился очень вкусный, и поэтому Крош хочет, чтобы ему достался кусок как можно большей площади. Помогите ему определить, какую максимальную площадь торта он сможет оставить себе.
Входные данные
Первая строка входных данных содержит единственное целое число n ( 1 ≤ n ≤ 4·10
4 ) — длину торта. Вторая строка входных данных содержит единственное целое число m ( 1 ≤ m ≤ 4·10
4 ) — ширину торта.
Гарантируется, что от торта Кроша можно отрезать два куска, оставив при этом прямоугольник ненулевой площади.
Выходные данные
Выведите одно число — максимальную площадь куска торта, который сможет оставить себе Крош.
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
4
3 |
6 |
Примечание
Иллюстрация к тесту из примера: Крош делает разрезы вдоль пунктирных линий, отдавая гостьям куски с серыми границами. В конце ему достается кусок размера 2 × 3 .