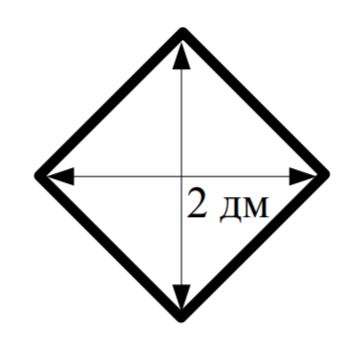
При проведении ремонта в квартире дизайнер предложил выложить стену узором из квадратных плиток, повернув их на 45°. Длина диагонали квадрата равна 2 дм.
Стена, которую необходимо покрыть плиткой, имеет размеры n × m дм, при этом числа n и m – целые чётные. Для покрытия такой стены необходимо какое-то количество целых квадратных плиток, а также несколько треугольных обрезков плитки. На рисунке на следующей странице приведён пример покрытия плиткой стены размером 4 × 6 дм, при этом было использовано 8 целых квадратных плиток.
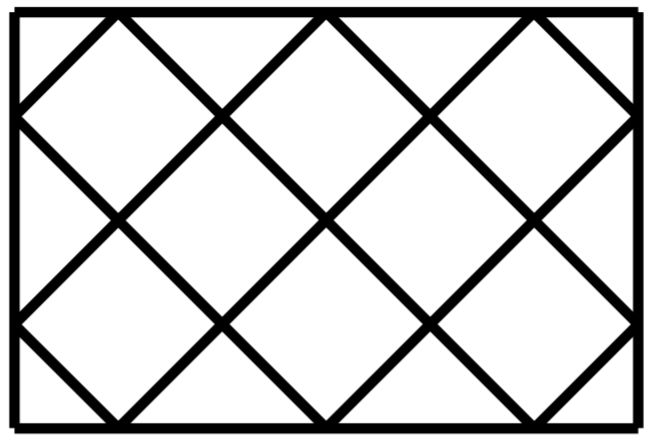
По данным размерам стены n и m дм определите, какое число целых квадратных плиток будет содержать такой узор.
Ответом на эту задачу является некоторое выражение, которое может содержать целые числа, переменные n и m (записываемые английскими буквами), операции сложения (обозначаются «+»), вычитания (обозначаются «−»), умножения (обозначаются «*»), деления (обозначаются «/») и круглые скобки для изменения порядка действий. Запись вида «2n» для обозначения произведения числа 2 и переменной n неверная, нужно писать «2 * n».
Ваше выражение должно давать правильный ответ для любых чётных значений n и m, например, для n = 4 и m = 6 значение выражения должно быть равно 8.
Пример правильной формы записи ответа.
m / 2 + (m * n − m) * 2