Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. Квадрат ограничен внешними стенами.
Перед каждым запуском Робота он обладает запасом энергии в 4000 единиц. В каждой клетке квадрата указано количество энергии, которое Робот потратит, перемещаясь в данную клетку; это также относится к начальной и конечной клеткам маршрута Робота. Помимо клеток, где Робот тратит энергию, на поле есть заправочные станции. Обозначены такие клетки отрицательными числами. Проходя через них, Робот пополняет свой запас энергии на величину, равную модулю числа, указанного в клетке заправочной станции.
Определите минимальный и максимальный запас энергии, который может остаться у Робота, после перемещения из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала минимальный запас энергии, затем максимальный.
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке квадрата. Внешние стены обозначены утолщенными линиями.
Пример входных данных:
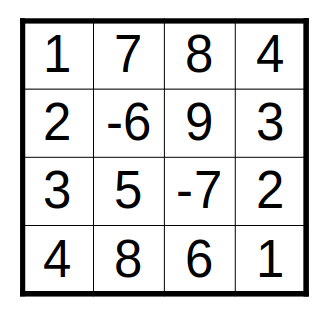
Если начальный запас энергии Робота равен 100 единиц, то для указанных входных данных ответом должна быть пара чисел: 69 102
Скачать файл