Квадрат разлинован на N × N клеток (1 < N < 26). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд:
вправо или
вниз. По команде
вправо Робот перемещается в соседнюю клетку правее текущей; по команде
вниз – в соседнюю нижнюю. Робот разрушается при попытке выхода за границу квадрата или при попытке пересечения стены клетки. В таблице стены отмечены границами с утолщением.
Перед запуском Робота в каждой клетке квадрата указан бонус, который Робот забирает после посещения клетки. Размер бонуса в каждой клетке – это натуральное число, не превышающее 100. Это правило относится к начальной и конечной клеткам маршрута Робота.
Определите минимальную и максимальную суммы бонусов, которые может собрать Робот, перемещаясь из левой верхней клетки квадрата в его правую нижнюю клетку. В ответе укажите два числа: сначала минимальную сумму, затем максимальную.
Исходные данные представлены в форме электронной таблицы размером N × N, в которой одна ячейка соответствует одной клетке квадрата. Стены, через которые Роботу нельзя проходить, отмечены в электронной таблице границами с утолщением.
Найденные числа запишите через пробел.
Пример входных данных:
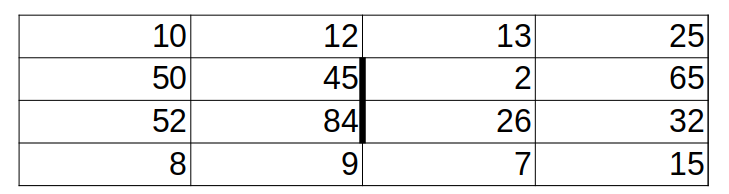
Для указанных входных данных ответом является пара чисел:
85 227
Скачать файл