Квадрат разлинован на N × N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение
одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз –
в соседнюю нижнюю. Квадрат ограничен внешними стенами. Между соседними клетками квадрата также могут быть внутренние
стены. Сквозь стену Робот пройти не может.
Перед каждым запуском Робота в каждой клетке квадрата лежит монета достоинством от 1 до 100. Посетив клетку, Робот забирает
монету с собой; это также относится к начальной и конечной клеткам маршрута Робота.
Определите максимальную и минимальную денежные суммы, которые может собрать Робот, пройдя из левой верхней клетки
в правую нижнюю. В ответе укажите два числа – сначала максимальную сумму, затем минимальную, через пробел.
Исходные данные представляют собой электронную таблицу размером N × N, каждая ячейка которой соответствует клетке
квадрата. Внутренние и внешние стены обозначены утолщёнными линиями.
Пример входных данных:
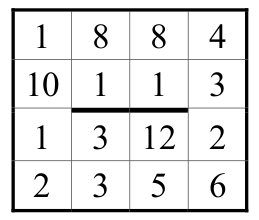Скачать файл