На координатной плоскости выбран прямоугольный участок, ограниченный осями координат и двумя прямыми, параллельными осям координат. Внутри данного участка распологается некоторое количество точек, координаты которых известны. Необходимо разместить внутри данного участка прямоугольник так, чтобы его стороны были параллельны осям координат, а площадь была максимально возможной. Ни одна точка не может оказаться внутри прямоугольника, но может быть на его границе.
Входные данные
Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке два натуральных числа A и B (1 ≤ A, B ≤ 10
4) через пробел – это длины сторон прямоугольника, лежащие соответственно на координатных осях OX и OY. Во второй строке входного файла записано натуральное число N – количество точек на участке (1 ≤ N ≤ 10
3). В каждой из последующих N строк записаны через пробел по два целых неотрицательных числа – координаты точек. Все точки попарно различны и располагаются внутри или на границе участка.
В качестве ответа необходимо найти периметр прямоугольника максимальной площади, который можно разместить на данном участке, так чтобы он не выходил за границы участка, и ни одна точка не оказалось внутри прямоугольника. Если существует несколько прямоугольников с максимальной площадью, то в качестве ответа нужно выбрать тот из них, который имеет минимальный периметр.
Пример организации исходных данных во входном файле:
5 5
6
2 2
1 4
3 1
3 4
2 1
4 3
Для указанных входных данных можно разместить прямоугольник площадью 8 (см. рисунок), периметр этого прямоугольника равен 12.
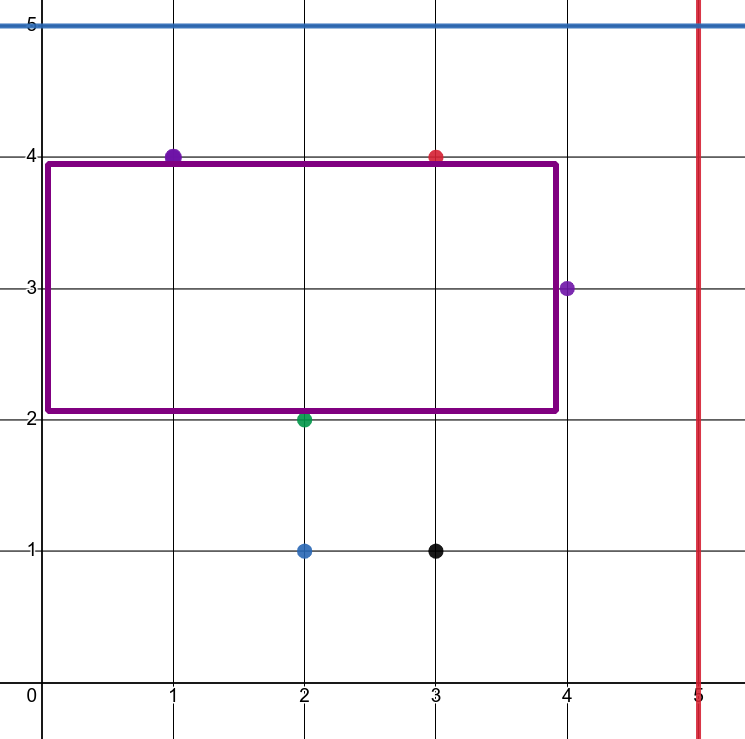
В ответе укажите два числа: значение периметра искомого прямоугольника сначала для файла А, затем для файла B.
Предупреждение: для обработки файла B не следует использовать переборный алгоритм для всех возможных вариантов, поскольку написанная по такому алгоритму программа будет выполняться слишком долго.
Файл А
Файл В