Дан массив \(a\) длины \(n\). Каждый элемент массива — \(-1\), \(0\) или \(1\). Известно, что \(-1\) находятся только строго в правой половине массива, то есть на индесах от \(\left\lfloor\frac{n + 1}{2}\right\rfloor + 1\) до \(n\). Все оставшиеся элементы могут быть равны только \(0\) или \(1\).
С массивом разрешается выполнять следующие два вида действий:
-
Заплатить две монеты и удалить из массива любое число \(a_i\). После такого действия массив \([a_1, a_2, \ldots, a_k]\) превращается в \([a_1, \ldots, a_{i-1}, a_{i+1}, \ldots, a_k]\).
-
Заплатить одну монету и заменить два стоящих рядом числа \(a_i\) и \(a_{i+1}\) на \(a_{i+1} + 1\) копию числа \(a_i\). То есть, возможны следующие преобразования:
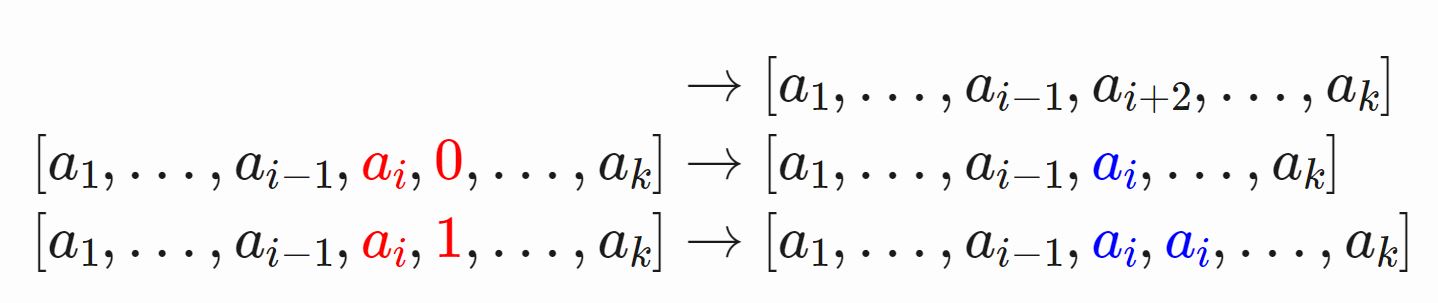
Иными словами, \(-1\) можно удалить вместе с предыдущим числом, \(0\) можно удалить сам по себе, если он стоит не в начале массива, а \(1\) можно заменить на предшествующее ей число.
Определите, какое минимальное число монет требуется заплатить, чтобы превратить данный массив в пустой. Обратите внимание, что ответ всегда существует, потому что можно просто \(n\) раз применить первую операцию.
Формат входных данных
В первой строке дано единственное целое число \(T\) — количество наборов входных данных (\(1 \le T \le 100\)). Далее следуют \(T\) наборов входных данных.
Каждый набор входных данных начинается со строки, содержащей единственное число \(n\) — изначальную длину массива. В следующей строке через пробел перечислены целые числа \(a_1\), …, \(a_n\) — элементы массива (\(-1 \le a_i \le 1\)).
Гарантируется, что сумма длин массивов по всем наборам входных данных не превосходит \(10^6\).
Формат выходных данных
Выведите \(T\) целых чисел, каждое в своей строке — ответы на задачу для каждого набора входных данных в том порядке, в котором оны даны во вводе.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4
7
1 1 0 0 -1 1 1
5
0 0 0 0 0
11
0 1 0 1 1 0 -1 1 1 0 -1
10
0 1 1 1 1 -1 1 0 1 0
|
6
6
9
11
|