Глеб обожает играть в го. Партия в го проходит на квадратной клетчатой доске размера n x n, на которую выкладываются белые и чёрные камни (в этой задаче, для удобства, камни будут находиться внутри клеток, хотя в оригинальной игре они выкладываются на пересечения линий доски). Проблема в том, что партия в го играется между двумя игроками, а у Глеба, к сожалению, совсем нет друзей (которые умеют играть в го). Так как поиграть Глебу все-таки хотелось, он придумал свои правила для го, в которых играет один человек, и предложил вам сыграть по его правилам.
Дана доска размера n x n, каждая клетка которой либо пустая, либо содержит черный камень. В вашем распоряжении есть
k белых камней, которые вы можете выложить на доску.
Говоря про соседние клетки в дальнейшем будем иметь в виду соседей сверху, снизу, справа или слева. Все камни одного цвета на доске делятся на
группы: два одноцветных камня находятся в одной группе, если от одного из них можно дойти до другого, перемещаясь по соседним клеткам, содержащим камни того же цвета (в частности, один камень, не имеющий соседних клеток с камнями того же цвета, образует группу из одного камня).
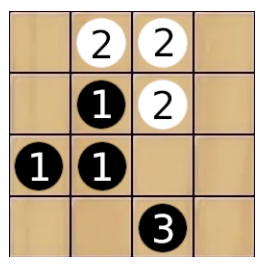
Рис. 1: На доске пронумерованы 3 группы камней: две чёрные и одна белая
Группа камней считается живой, если хотя бы у одного камня из группы есть соседняя пустая клетка; в противном случае группа камней считается мёртвой.
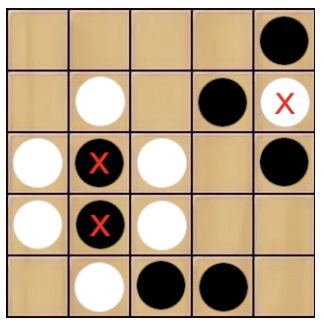
Рис. 2: Мёртвые камни на доске выделены крестиком
Вы можете выложить на доску
не более k белых камней, класть камень можно только в пустую клетку, в одной клетке не может находиться два камня. После того, как вы их выложите, происходит подсчёјт очков: сначала с доски снимаются все мёртвые белые группы камней, после чего снимаются оставшиеся мёртвые чёрные группы камней (заметьте, что некоторые чёрные группы могут "ожить" после снятия белых камней, и сняты уже не будут). Результатом игры для вас является количество снятых с доски чёрных камней, и ваша задача - максимизировать его.
В первой строке входных данных записано число
t количество наборов входных данных. Далее следуют описания наборов.
В первой строке набора вводятся два числа
n и
k размер доски и количество доступных белых камней. Далее вводятся
n строк, по
n символов в каждой, описывающие состояние доски: клетка с координатами
(i, j) либо пустая (в строке
i на позиции
j стоит символ "
."), либо содержит чёрный камень (в строке
i на позиции
j стоит символ "
*").
Для каждого набора в первой строке выведите число
n ≤ k количество использованных белых камней. В последующих
m строках выведите через пробел координаты клеток, в которые вы поставили белые камни, в произвольном порядке. Координаты клеток нумеруются с единицы, все выведенные координаты должны быть различными, на месте выведенных координат не должно быть чёрных камней.
В этой задаче t = 7. Оценка за этот тест: 70 баллов. За каждый правильный набор можно получить до 10 баллов. Оценка за каждый набор будет вычисляться по формуле
10·(participant_ans/jury_ans )7, где
jury_ans - максимальное количество снятых чёрных камней в решениях жюри и всех участников, а
participant_ans - количество снятых чёрных камней в решении участника. Проверка осуществляется в режиме offline (результат виден после окончания тура).
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
1
4 5
*..*
*...
..**
....
|
5
1 2
2 2
3 1
1 3
2 4
|