При подготовке олимпиад у каждого разработчика есть своя зона ответственности. Обычно каждый разработчик полностью отвечает за подготовку какой-то определенной задачи, однако в этот раз жюри ИОИП решило поступить по-другому.
Всего в команде разработчиков \(n\) человек. Также есть \(n\) задач, которые необходимо подготовить. Подготовка \(i\)-й задачи требует подготовки ровно \(c_i\) ее элементов, и разработка каждого элемента \(i\)-й задачи имеет сложность \(w_i\).
Было решено, что каждый разработчик будет отвечать за столько же элементов, за сколько он бы отвечал, если бы разрабатывал целиком соответствующую задачу. Иными словами, \(i\)-му разработчику будет назначено ровно \(c_i\) элементов из различных задач. Распределение элементов по разработчикам происходит следующим образом:
-
Сначала первому разработчику выдается \(c_1\) элементов, затем второму — \(c_2\), и так далее. Переход к \((i+1)\)-му разработчику происходит в тот момент, когда \(i\)-му назначается ровно \(c_i\) элементов.
-
Элементы, за которые будет отвечать каждый разработчик, выбираются по одному из всех еще не до конца распределенных задач по очереди. Сначала будет выбран один этап из первой задачи, затем — из второй, из третьей, и так далее по кругу. Если в какой-то задаче не осталось нераспределенных этапов, она пропускается.
-
Элементы, назначаемые очередному разработчику, выбираются начиная с той задачи, на которой остановился предыдущий разработчик. То есть, если последний элемент, назначенный предыдущему разработчику, был из \(x\)-й задачи, то первый элемент, назначенный следующему, будет из задачи \((x+1) \bmod n\) (если в ней еще остались нераспределенные элементы).
Иными словами, поддерживается набор еще не до конца распределенных задач и указатель \(x\) на <<текущую>> задачу. Когда надо выдать текущему разработчику очередной элемент, ему выдается один элемент из задачи \(x\), после чего \(x\) сдвигается по кругу вперед на следующую задачу.
Жюри считает, что такой способ позволяет более честно распределить сложность подготовки олимпиады. Определите суммарную сложность разработки элементов, доставшихся каждому из \(n\) разработчиков.
Формат входных данных
В первой строке дано целое число \(n\) — количество разработчиков (\(1 \le n \le 500\,000\)).
В \(i\)-й из следующих \(n\) строк через пробел даны два целых числа \(c_i\) и \(w_i\) — количество элементов в \(i\)-й задаче и сложность их разработки (\(1 \le c_i, w_i \le 10^9\)).
Формат выходных данных
В единственной строке выведите через пробел \(n\) чисел, \(i\)-е из которых равно суммарной сложности разработки элементов, доставшихся \(i\)-му разработчику.
Замечание
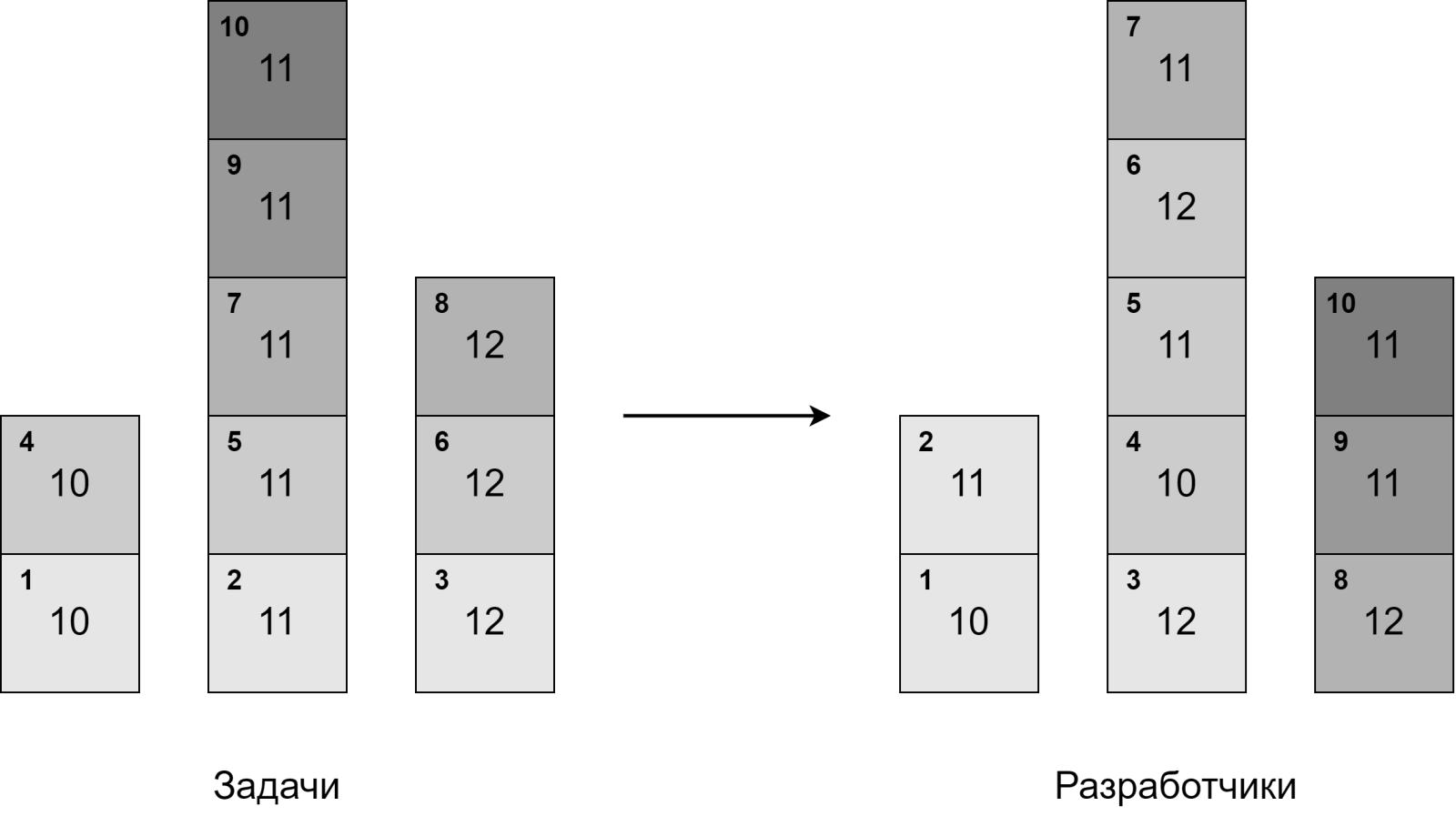
Иллюстрацию к третьему примеру можно видеть ниже. Слева показаны элементы, из которых состоят задачи, справа — элементы, назначенные каждому разработчику.
В центре каждого элемента указана сложность его реализации, а число в левом верхнем углу обозначает порядок выбора элементов. Элементы выбираются из задач в порядке слева-направо, затем снизу-вверх, а назначаются в порядке снизу-вверх, затем слева-направо.