Коллайдер — это установка для изучения столкновений элементарных частиц. При его работе частицы разгоняются до большой скорости. Специальный детектор позволяет фиксировать траектории частиц в виде прямых на горизонтальной плоскости.
На детектор сверху направлена сверхскоростная камера на вращающемся в горизонтальной плоскости креплении. Ориентация камеры в каждый момент времени задаётся направляющей прямой. Камера может сфотографировать произвольную прямоугольную область, одна из сторон которой параллельна заданной направляющей прямой.
Для анализа потенциальных столкновений частиц важно, чтобы на каждом фотоснимке были отображены все точки пересечений их траекторий. Камера использует очень дорогие расходные материалы, поэтому площадь каждого фотоснимка необходимо минимизировать.
Требуется написать программу, которая по хронологической последовательности событий двух типов:
-
появление новой траектории частицы,
-
получение фотоснимка камерой, ориентированной по заданной направляющей прямой,
определит для каждого фотоснимка минимальную площадь прямоугольной области, включающей все точки пересечения траекторий частиц, появившихся до этого снимка.
Формат входных данных
В первой строке задано одно целое число \(n\) (\(1 \leqslant n \leqslant 200\,000\)) — общее количество событий. В следующих \(n\) строках заданы описания событий.
Описание каждого события состоит из пяти элементов. Первый элемент является символом <<+>>, если это событие является появлением новой траектории, или символом <<?>>, если это событие является получением фотоснимка. Последующие четыре элемента — целые числа \(x_1\), \(y_1\), \(x_2\), \(y_2\) (\(-10\,000 \leqslant x_1, y_1, x_2, y_2 \leqslant 10\,000\)) — координаты двух несовпадающих точек. Для событий первого типа указанные точки лежат на траектории частицы. Все траектории различны. Для событий второго типа указанные точки лежат на направляющей прямой камеры.
Формат выходных данных
Пусть \(q\) — количество полученных фотоснимков. Выходной файл должен содержать \(q\) вещественных чисел — минимальные возможные площади фотоснимков, перечисленные в порядке их получения камерой. Тест будет успешно пройден, если для каждой из \(q\) выведенных площадей выполняется условие \(\frac{|a - b|}{\max(1, b)} \leqslant 10^{-4}\), где \(a\) — площадь, выведенная участником, \(b\) — площадь, полученная решением жюри.
Примеры
| № |
Входные данные |
Выходные данные |
Иллюстрация |
| 1 |
6
+ 0 0 0 1
+ 0 0 1 0
+ 1 0 0 2
? 0 0 0 1
+ 2 4 3 6
? 0 0 1 1 |
2.0
3.000 |
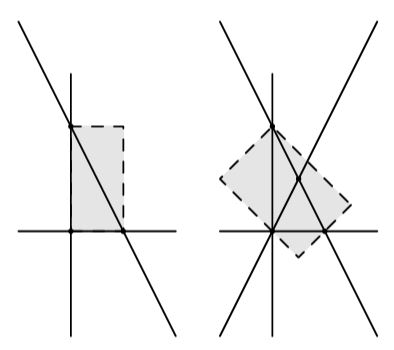 |
| 2 |
7
? 11 4 -7 8
+ -2 -2 1 1
? 0 0 0 1
+ 0 1 1 0
+ 0 2 2 0
? 0 0 0 1
? 0 0 1 1
|
0.0
0.0
0.25
0.0000000
|
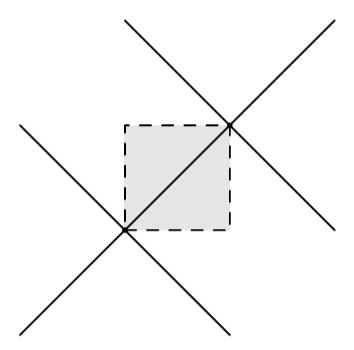 |