Недавно Билл устроился на работу полицейским. Теперь ему предстоит каждый вечер обходить свой участок, который представляет собой прямоугольник, состоящий из N×M кварталов. Каждый квартал имеет вид квадрата размером 100×100 метров, кварталы отделены друг от друга прямыми улицами.
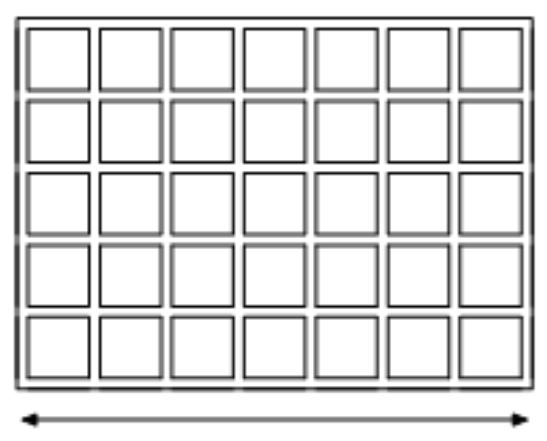
Таким образом, через участок Билла проходит N + 1 улица, идущая с запада на восток и M + 1 улица, идущая с севера на юг. Перекрестки разбивают улицы на (N + 1)M + (M + 1) N отрезков, каждый из которых имеет длину 100 метров.
Совершая обход, Билл выходит из полицейского управления, расположенного около юго-западного угла его участка, обходит свой участок и возвращается в управление. Во время обхода Билл должен пройти по каждому отрезку улицы на территории своего участка как минимум один раз. Известно, что во время обхода Билл проходит отрезок длиной 100 метров за одну минуту. Выясните, какое минимальное число минут потребуется Биллу, чтобы совершить обход.
Входные данные
Вводятся целые числа N и M, разделенные пробелом (1≤N, M≤10 000).
Выходные данные
Выведите минимальное время, за которое Билл может совершить обход.
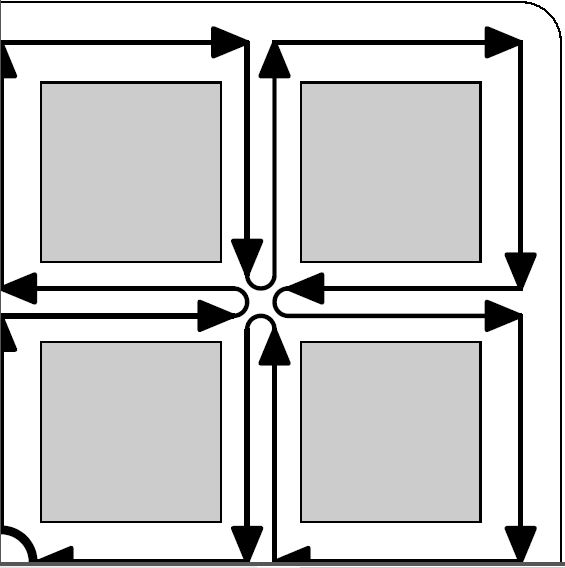
Пояснение ко второму примеру
Один из возможных оптимальных путей для Билла во втором примере показан на рисунке.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
1 1
|
4
|
|
2
|
2 2
|
16
|
|
3
|
3 4
|
38
|