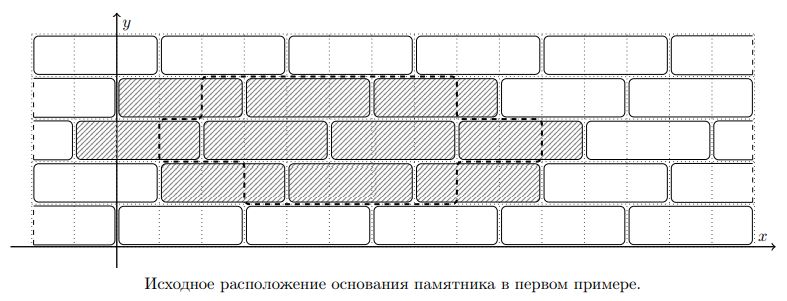
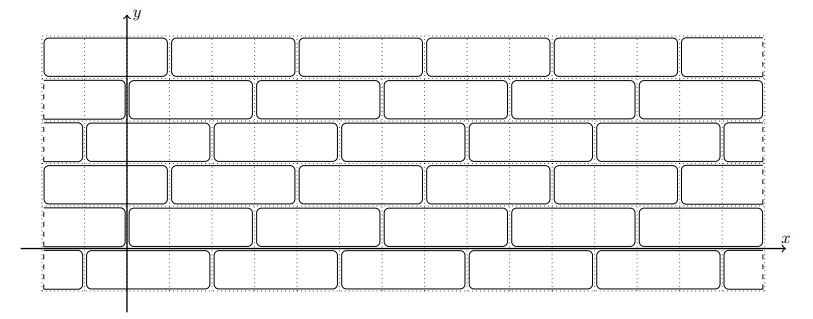
Одна из центральных площадей Архангельска замощена прямоугольными плитками размера \(1 \times k\). Если ввести систему координат, так что левый нижний угол одной из плиток будет иметь координаты \((0, 0)\), то левые нижние углы плиток будут иметь координаты \((i \cdot k+j,j)\) для всех целых \(i\) и \(j\).
На площади было решено установить памятник известному архангельскому писателю и художнику Писахову. Для установки памятника необходимо удалить все плитки, полностью или частично попадающие под его основание. Основание памятника имеет форму многоугольника с целочисленными координатами вершин, все стороны которого параллельны осям координат. Известно, что любая прямая, пересекающая основание памятника и параллельная одной из осей координат, в пересечении с основанием образует один отрезок.
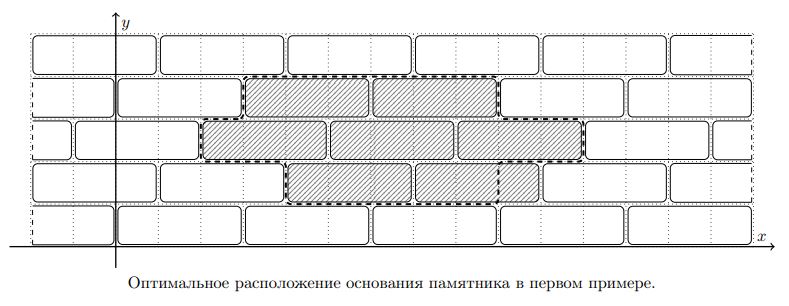
Для установки памятника необходимо выбрать место на площади таким образом, чтобы количество удалённых плиток было минимальным. При выборе места основание разрешается только передвигать параллельно осям координат.
Требуется написать программу, вычисляющую минимальное количество плиток, которые придётся .
Входные данные
Первая строка входных данных содержит два числа \(n\) и \(k\) — количество вершин в основании памятника и размер плитки.
Каждая из последующих \(n\) строк содержит два целых числа \(x_i\), \(y_i\) — координаты \(i\)-й вершины основания. Координаты перечислены в порядке обхода против часовой стрелки.
Выходные данные
Единственная строка выходных данных должна содержать минимально возможное количество плиток, которые необходимо удалить для размещения памятника на площади.
Замечание