Жители Зожбурга очень любят спорт и в особенности бег. Бегать обычные марафоны им надоело, поэтому они решили организовать прямоугольный забег в стиле Minecraft. Для этого на центральной площади города оборудовали стадион с прямоугольным газоном и дорожками вокруг него. Жители Зожбурга считают, что главное — не победа, а участие, поэтому цель забега — сделать красивую фотографию, а не пробежать быстрее всех.
Центральная площадь Зожбурга представляет собой прямоугольник, разделенный на одинаковые единичные квадраты. Строки пронумерованы сверху вниз с единицы, столбцы слева направо с единицы. Каждый квадрат площади имеет координаты \(r\) и \(c\) — номер строки и столбца, соответственно.
На площади находится прямоугольный газон со сторонами, параллельными сторонам площади. Координаты левого верхнего углового квадрата газона \((R_L, C_L)\), координаты правого нижнего углового квадрата газона \((R_R, C_R)\). Вокруг газона оборудованы \(n\) дорожек для \(n\) бегунов. Дорожка \(i\) находится на расстоянии \(i\) от границы газона, на дорожке \(i\) находится бегун с номером \(i\). Бегун \(i\) стартует с квадрата с координатами \((r_i, c_i)\). Бегуны стартуют одновременно с одинаковой скоростью: через каждую секунду каждый спорстмен меняет текущий квадрат на своей дорожке на следующий квадрат на своей дорожке в направлении против часовой стрелки.
На прямоугольном газоне в квадрате \((R_p, C_p)\) стоит фотограф, цель которого — сделать красивую фотографию. Фотограф тестирует инновационную камеру с двойным объективом. Эта камера делает снимок одновременно в двух противоположных направлениях. Фотограф считает фотографию красивой, если все бегуны в момент, когда он делает снимок, находятся в одновременно в строке \(R_p\) или в стоблце \(C_p\). При этом благодаря инновационному свойству камеры они могут быть либо в одной строке с ним и справа и слева от него, либо в одном столбце с фотографом и выше и ниже него.
Ваша задача — узнать, через какое минимальное количество секунд \(t\) после старта забега фотограф сможет сделать красивую фотографию, или сказать, что красивая фотография в данных условиях не получится.
Формат входных данных
В первой строке входных данных находится число \(n\) (\(1 \le n \le 18\)) — количество бегунов. В следующей строке ввода даны шесть целых чисел \(R_L\), \(C_L\), \(R_R\), \(C_R\) (\(n + 1 \le R_L \le R_R \le 100 - n\), \(n + 1 \le C_L \le C_R \le 100 - n\)), \(R_p\) (\(R_L \le R_p \le R_R\)), \(C_p\) (\(C_L \le C_p \le C_R\)) — координаты левого верхнего квадрата газона, правого нижнего квадрата газона, координаты фотографа, соответственно. Гарантируется, что \(R_R - R_L + C_R - C_L\) делится на \(4\).
В следующих \(n\) строках даны два числа \(r_i\), \(c_i\) — стартовые координаты бегуна \(i\). Гарантируется, что стартовые координаты бегуна \(i\) находятся на дорожке \(i\), на каждой дорожке находится один бегун, дорожка \(i\) находится на расстоянии \(i\) от границы газона.
Формат выходных данных
Выведите единственное число \(t\) — через какое минимальное количество секунд \(t\) после старта забега фотограф сможет сделать красивую фотографию, или \(-1\), если фотографию сделать не получится.
Рисунок ко второму примеру.
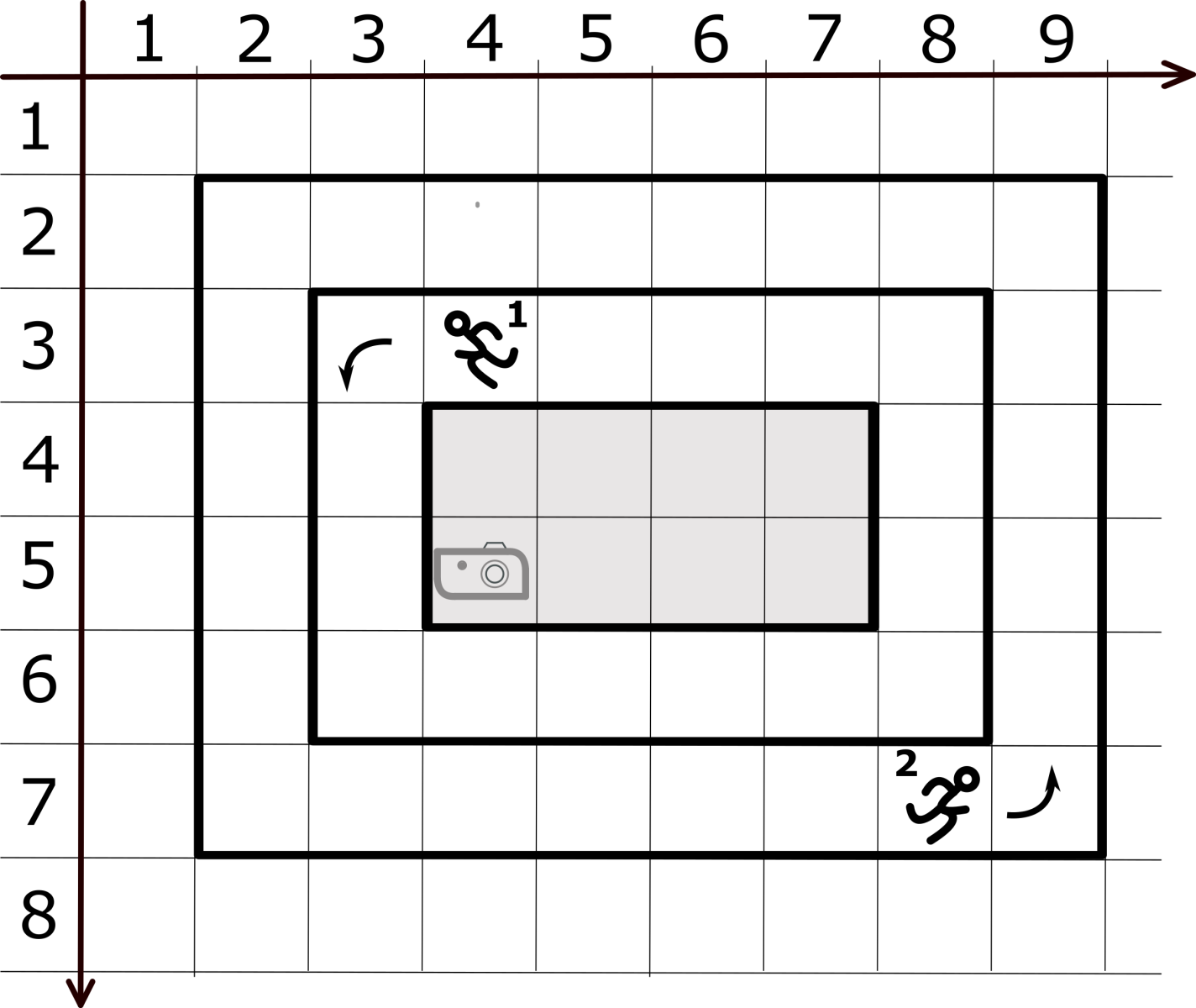
Стартовое положение бегунов.
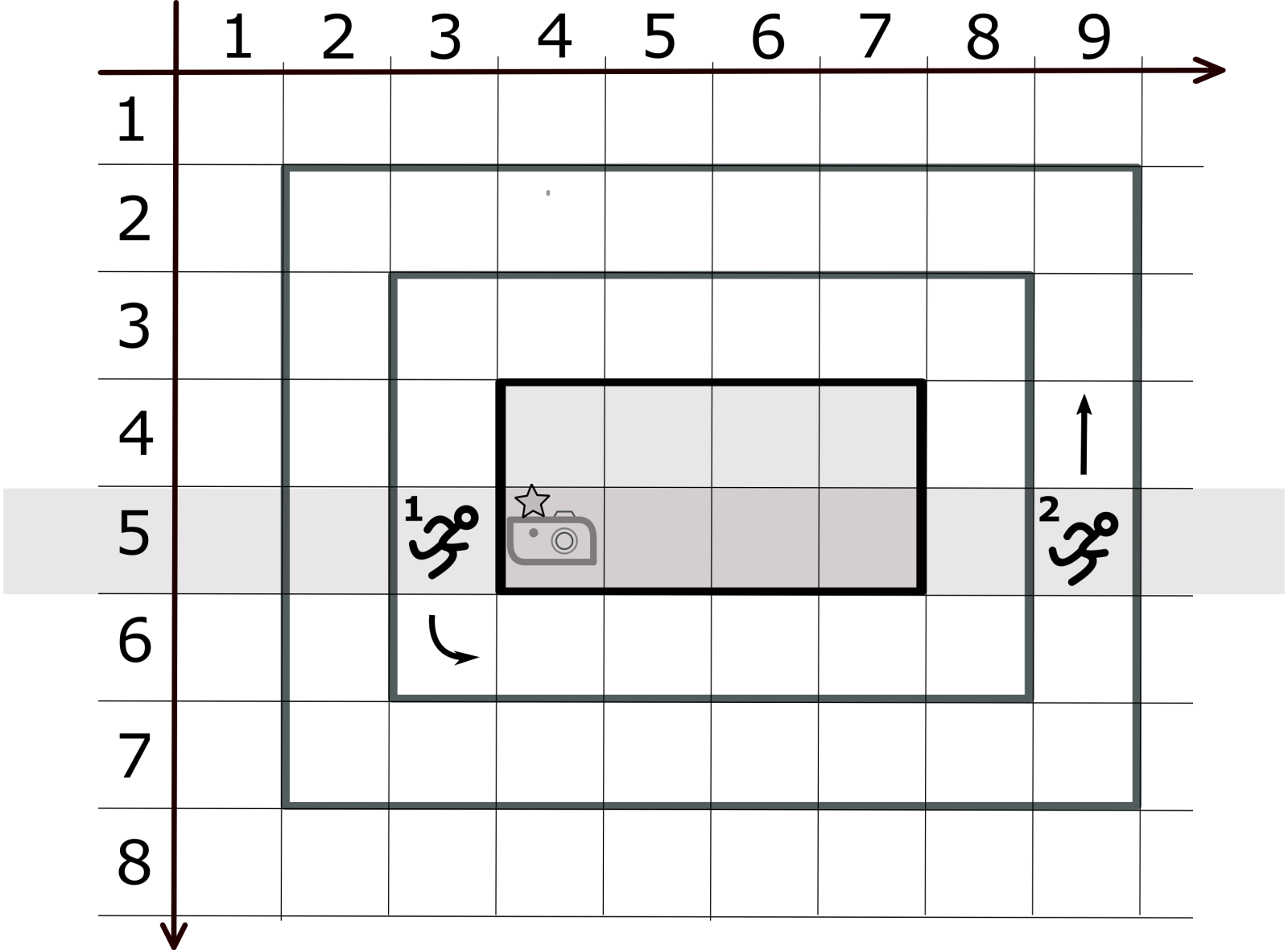
Положение бегунов через 3 секунды. Все бегуны находятся в строке \(R_p\), и фотограф делает красивое фото.
Примеры
| № | Входные данные | Выходные данные |
|
1
|
2
3 3 5 5 4 3
2 3
1 1
|
3
|
|
2
|
2
4 4 5 7 5 4
3 4
7 8
|
3
|