Количество элементов во множестве
Предположим, что множество A содержит 10 элементов, множество B — 15 элементов, а их пересечение (множество A · B ) — два элемента. Как определить, сколько элементов содержится во множестве A + B?
Попробуем рассмотреть задачу в общем виде и вывести формулу для её решения. Обозначим через NX число элементов в области X. Далее операцию И будет обозначать символом &, а операцию ИЛИ — символом | (именно эти символы используются в поисковых запросах в Интернете).
Построим диаграмму с двумя областями — A и B. Эти области могут быть разделены или пересекаться.
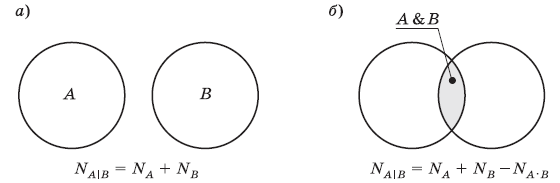
В первом случае, когда области не пересекаются, получаем очевидную формулу:
NA | B = NA + NB.
Во втором случае в сумму NA + NB общие элементы (элементы множества NA&B) входят дважды. Поэтому, чтобы получить количество элементов в объединении множеств, нужно из этой суммы вычесть число общих элементов:
N A|B = NA + NB – NA&B.
Эта формула, которую называют формулой включений и исключений, справедлива и для рисунка а, где NA&B = 0.
Для трех множеств эта формула принимает вид:
N A|B|C = NA + NB + NC – NA&B – NB&C – NC&A + NA&B&C
Сложные запросы в поисковых системах
Для решения задач, в которых используются множества, например множества страниц, полученных от поисковой системы
в ответ на какой-то запрос, удобно применять диаграммы Эйлера–Венна.
Задача 1. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию И, а «|» — операцию ИЛИ):
собаки | кошки 770
кошки 550
собаки & кошки 100
Сколько страниц будет найдено по запросу собаки?
Введём два множества: A — множество страниц, где есть слово «собаки», B — множество страниц со словом «кошки». По формуле включений и исключений получаем:
NA = NA|B – N B + NA&B = 770 – 550 + 100 = 320.
Задача 2. Известно количество страниц, которые находит поисковый сервер по следующим запросам:
собаки & лемуры 320
кошки & лемуры 280
(кошки | собаки) & лемуры 430
Сколько страниц будет найдено по запросу
кошки & собаки & лемуры?
Заметим, что во всех запросах есть часть & лемуры. Это означает, что область поиска во всех случаях ограничена страницами, на которых встречается слово «лемуры».
Обозначим буквами С, К и Л области (группы страниц), содержащие ключевые слова «собаки», «кошки» и «лемуры» соответственно. Нас интересует только область, выделенная фоном на рисунке.
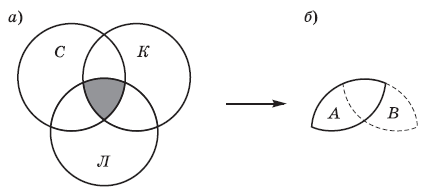
Эта область образована в результате пересечения двух областей рисунок б):
A = собаки & лемуры
B = кошки & лемуры
Поэтому задачу можно свести к задаче с двумя областями.
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
A 320
B 280
A | B 430
Сколько страниц будет выдано по запросу A & B?
Используя формулу включений и исключений, полученную в предыдущем пункте, находим:
NA&B = NA + N B – N A|B = 320 + 280 – 430 = 170.
Задачу с тремя областями не всегда удаётся свести к более простой задаче с двумя областями. Серьёзным упрощением может стать то, что какие-то два множества не имеют общих элементов.
Задача 3. Известно количество страниц, которые находит поисковый сервер по следующим запросам:
собаки 200
кошки 250
лемуры 450
кошки | собаки 450
кошки & лемуры 40
собаки & лемуры 50
Сколько страниц найдёт этот сервер по запросу
(кошки | собаки) & лемуры?
Здесь часть & лемуры встречается не во всех запросах, поэтому свести задачу к задаче с двумя областями не удаётся. Используя те же обозначения, что и в задаче 2, построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу
(кошки | собаки) & лемуры.
На рисунке эта область выделена фоном.
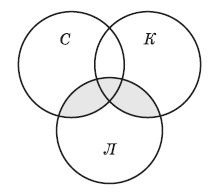
В общем виде задача с тремя областями очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия:
собаки 200
кошки 250
кошки | собаки 450
Это означает, что область кошки | собаки равна сумме областей кошки и собаки, т. е. эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит так (Микки Маус), что значительно упрощает решение.
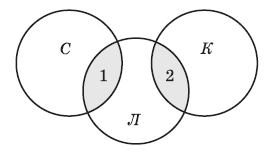
Размеры областей 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 страниц, поэтому по запросу
(кошки | собаки) & лемуры
поисковый сервер найдёт 40 + 50 = 90 страниц.
В общем случае задачи решаются с использованием систем уравнений.
Рассмотрим это на примере.
Задача 4. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос |
Количество страниц (тыс.) |
| Робот & (Ум | Интеллект) |
100 |
| Ум & Робот |
60 |
| Ум |
210 |
| Интеллект & Робот |
70 |
| Интеллект |
200 |
| ~Робот & Ум & Интеллект |
20 |
Сколько страниц (в тысячах) будет найдено по запросу Ум | Интеллект?
Решение:
1) нарисуем диаграмму Эйлера-Венна для трёх областей (Р – Робот, У – Ум, И – Интеллект):
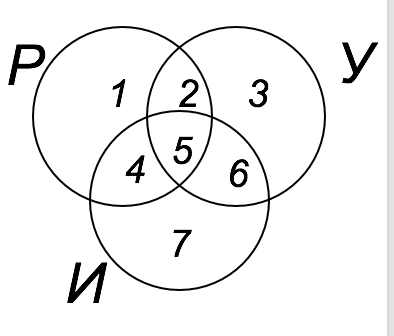
2) будем обозначать через N
x число найденных элементов в области с номером X
3) запишем области, которые фигурируют в запросах, как сумму непересекающихся областей, и выпишем равенства, которые следуют из данных в таблице:
| Запрос |
|
|
|
№ |
| Робот & (Ум | Интеллект) |
2 + 4 + 5 |
N2 + N4 + N5 = |
100 |
(1) |
| Ум & Робот |
2 + 5 |
N2 + N5 = |
60 |
(2) |
| Ум |
2+ 3 + 5 + 6 |
N2 + N3 + N5+ N6 = |
210 |
(3) |
| Интеллект & Робот |
4 + 5 |
N4 + N5 = |
70 |
(4) |
| Интеллект |
4 + 5 + 6 + 7 |
N4 + N5 + N6+ N7 = |
200 |
(5) |
| ~Робот & Ум & Интеллект |
6 |
N6 = |
20 |
(6) |
| Ум | Интеллект |
2 + 3 +
4 + 5 + 6 + 7 |
N2 + N3 +
N4 + N5 + N6+ N7 = |
X |
(7) |
4) подставляя (5) в (7), получаем
5) X = N2 + N3 + N4 + N5 + N6+ N7 = N2 + N3 + 200
6) из (3) находим N2 + N3 = 210 – N5 – N6 = 210 – N5 – 20 = 190 – N5
7) вычитая (1) из (4), получаем N2 = 30, и из (2) находим N5 = 60 – N2 = 30
8) тогда X = N2 + N3 + 200 = 190 – 30 + 200 = 360.
Ответ: 360.