Треугольники Паскаля и Лейбница

Пусть есть "линейная" последовательность  A={a₁, a₂, ..., a_n, ...} 
На основании последовательности A можно определить "треугольник  Лейбница" L_A = { T_i,j / i = 1,2, ...; j = 1, ..., i}  положив:

• T_i,1 =  a_i 
• T_i,j = T_i+1,j-1 + T_i+1,j    для 1 < j <= i

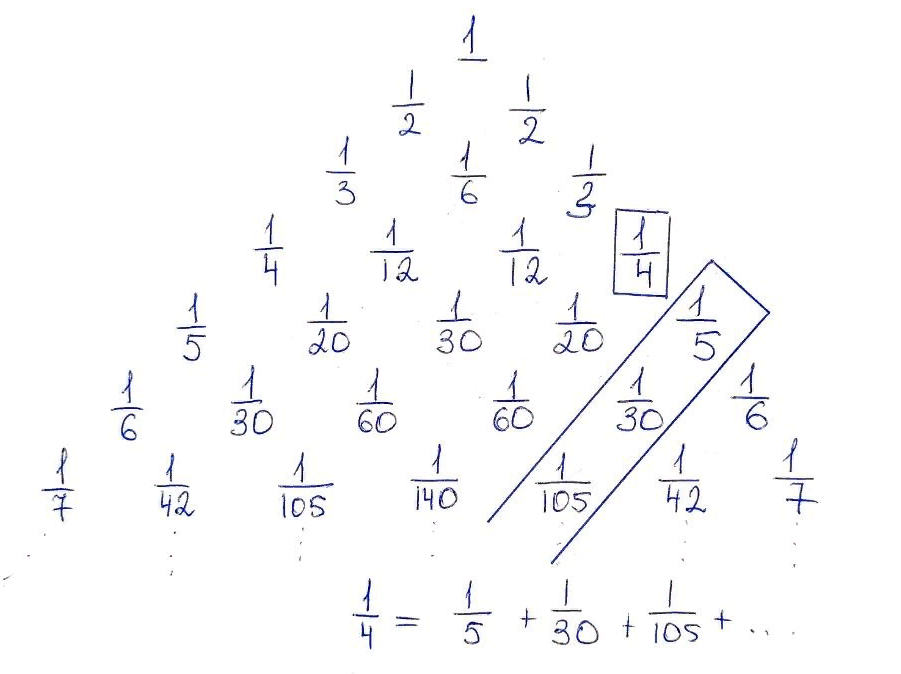
Если \(A = 1, \frac{1}{2},\frac{1}{3},\dots,\frac{1}{n},\dots\) то получим гарманический треугольник Лейбница
Любой элемент этого треугольника равен сумме (бесконечной) всех элементов, стоящих ниже его по любой из диагоналей
Треугольник Лейбница хорошо иллюстрирует схему Бернули, для этого А надо положить геометрической прогрессии 

Нетрудно заметить, что треугольник Лейбница полностью определяется "левой крайней гранью" и может может быть легко восстановлен по её значениям.  Попробуйте выполнить такое восстановление в табличном редакторе и проверьте себя с помощью компьютера.