Рассмотрим шахматную доску размера
N×N с множеством слонов, принадлежащих двум игрокам.
Слоны могут атаковать фигуры, стоящие на одной с ними диагонали в пределах шахматной доски.
На шахматном поле раставлены слоны белого и черного цвета. Ваша задача определить количество полей, в которых
безопасно можно разместить белого короля.
Поле называется безопасным, если оно не находиться под ударом фигур противника.
Входные данные
- 1 строка содержит три числа:
- N - размер доски ( 4 <= N <= 1000);
- Kw - количество белых слонов ( 0 <= Kw =< 2N );
- Kb - количество черных слонов ( 0 <= Kb =< 2N ):
- следующие Kw строк содержат позиции дружественных (белых) слонов
- следующие Kb строк содержат позиции недружественных (черных) слонов
Позиции фигур задаются числами x, y (0<= x, y < N), где x - номер вертикали, а y - горизонтали. Начало отсчета левый нижний угол.
Гарантируется, что позиции всех фигур находятся внутри доски и различны.
Выходные данные
Одно число - количество безопасных полей дла размещения белого короля
Пример входных данных и расстановки фигур
| Входные данные |
Выходные данные |
Начальная расстановка фигур |
Возможные поля для короля |
8 4 6
5 5
6 4
4 2
1 5
6 5
5 7
7 3
2 3
1 6
3 2 |
21 |
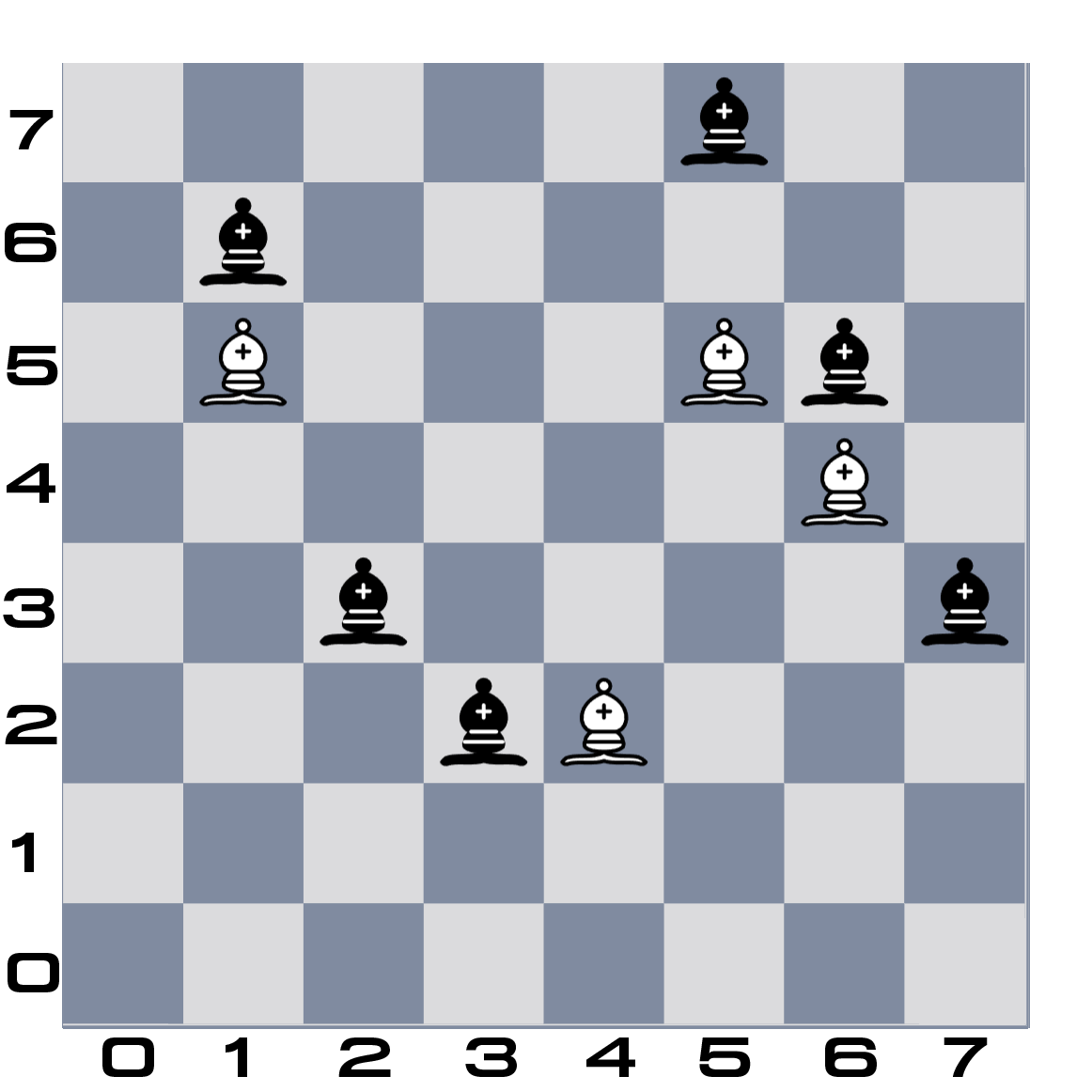 |
 |
| Некоторые ожидаемые результаты |
Параметры задания
(Размер, позиции белых слонов, позиции черных слонов) |
Ожидаемый результат |
22
(2, 1), (1, 15), (11, 5)
(1, 11), (3, 6) |
429 |
9
(2, 4)
(5, 3), (4, 0) |
58 |
4
(3, 2)
(1, 2) |
9 |
7
(1, 4)
(3, 2), (2, 1), (5, 2) |
30 |