Аня занимается рукоделием. Сегодня она решила связать платок из полупрозрачных ниток. Каждая нитка характеризуется единственным целым числом — коэффициентом прозрачности.
Платок делается по следующей схеме: выбираются горизонтальные нитки с коэффициентами прозрачности \(a_1, a_2, \ldots, a_n\) и вертикальные с коэффициентами прозрачности \(b_1, b_2, \ldots, b_m\). Затем они переплетаются между собой, как показано на картинке снизу, и образуют кусок ткани размера \(n \times m\), состоящий ровно из \(nm\) узлов:
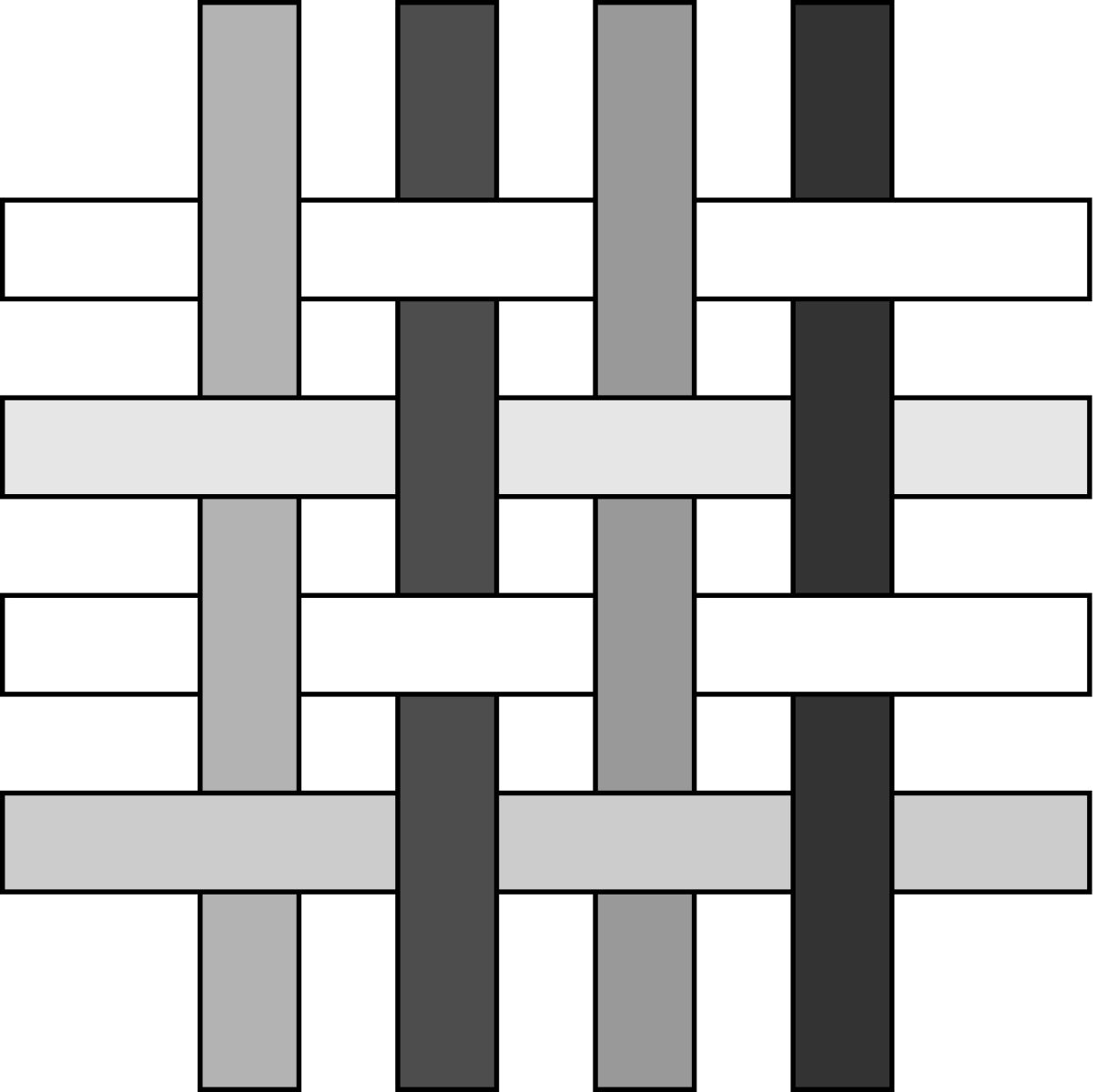
Пример куска ткани при \(n = m = 4\).
После того, как сплетение затянется и не будет видно зазоров между нитками, каждый узел, образованный горизонтальной ниткой с номером \(i\) и вертикальной ниткой с номером \(j\), превратится в клетку, которую мы будем обозначать как \((i, j)\). Клетка \((i, j)\) будет иметь коэффициент прозрачности \(a_i + b_j\).
\(^{\dagger}\)Подквадратом куска ткани называется множество всех его клеток \((i, j)\), таких что \(x_0 \le i \le x_0 + d\) и \(y_0 \le j \le y_0 + d\) для некоторых целых чисел \(x_0\), \(y_0\) и \(d\) (\(1 \le x_0 \le n - d\), \(1 \le y_0 \le m - d\), \(d \ge 0\)).
Интересностью полученного платка будем называть количество его подквадратов\(^{\dagger}\), в которых нет пары соседних по горизонтали или по вертикали клеток с одинаковыми коэффициентами прозрачности.
Аня ещё не решила, из каких ниток плести платок, поэтому вам будут даны также \(q\) запросов изменения коэффициентов прозрачности ниток на некотором отрезке, после каждого из которых надо вывести интересность полученного платка.
Формат входных данных
Первая строка содержит три целых числа \(n\), \(m\) и \(q\) (\(1 \le n, m \le 300\,000\), \(0 \le q \le 300\,000\)) — количество горизонтальных ниток, количество вертикальных ниток и количество запросов изменения.
Вторая строка содержит \(n\) целых чисел \(a_1, a_2, \ldots, a_n\) (\(-10^9 \le a_i \le 10^9\)) — коэффициенты прозрачности для горизонтальных ниток, нитки пронумерованы сверху-вниз.
Третья строка содержит \(m\) целых чисел \(b_1, b_2, \ldots, b_m\) (\(-10^9 \le b_i \le 10^9\)) — коэффициенты прозрачности для вертикальных ниток, нитки пронумерованы слева-направо.
В последующих \(q\) строках указаны запросы изменения. Каждый из запросов описывается четверкой целых чисел \(t\), \(l\), \(r\) и \(x\) (\(1 \le t \le 2\), \(l \le r\), \(-10^9 \le x \le 10^9\)). В зависимости от параметра \(t\) в запросе требуется сделать следующее:
-
\(t=1\). Коэффициенты прозрачности для горизонтальных ниток на отрезке \([l, r]\) увеличиваются на \(x\) (иными словами, для всех целых \(l \le i \le r\) значение \(a_i\) увеличивается на \(x\));
-
\(t=2\). Коэффициенты прозрачности для вертикальных ниток на отрезке \([l, r]\) увеличиваются на \(x\) (иными словами, для всех целых \(l \le i \le r\) значение \(b_i\) увеличивается на \(x\)).
Формат выходных данных
Выведите \((q+1)\) строку. В \((i + 1)\)-й строке (\(0 \le i \le q\)) выведите одно целое число — интересность платка после применения первых \(i\) запросов.
Примечание
В первом примере коэффициенты прозрачности клеток в получившемся платке равны:
Тогда есть следующие подквадраты, не содержащие двух соседних по вертикали или по горизонтали клеток с одинаковым коэффициентом прозрачности:
-
Каждая из \(16\) клеток по отдельности;
-
Подквадрат с левым верхним углом в клетке \((3, 1)\) и правим нижним углом в клетке \((4, 2)\);
-
Подквадрат с левым верхним углом в клетке \((2, 3)\) и правим нижним углом в клетке \((3, 4)\);
-
Подквадрат с левым верхним углом в клетке \((2, 1)\) и правым нижним углом в клетке \((3, 2)\);
-
Подквадрат с левым верхним углом в клетке \((3, 3)\) и правим нижним углом в клетке \((4, 4)\).
Во втором примере после первого запроса коэффициенты прозрачности горизонтальных ниток равны \([1, 2, 2]\). После второго запроса коэффициенты прозрачности вертикальных ниток равны \([2, -4, 2]\).
Примеры
| № | Входные данные | Выходные данные |
|
1
|
4 4 0
1 1 2 3
1 2 2 3
|
20
|
|
2
|
3 3 2
1 1 1
2 2 8
1 2 3 1
2 2 3 -6
|
9
10
11
|
|
3
|
3 2 2
-1000000000 0 1000000000
-1000000000 1000000000
1 1 1 1000000000
2 2 2 -1000000000
|
8
7
7
|