Задачи со сложностями - разбор

Черепашка рисует треугольник  Обычно, задачи про треугольник вызывают ужас у детей и сложности у учителей. Решать пытаюся

• "рисованием и подсчётом точек" вручную
• методом "сканирующей прямой"
• уравнениями прямых

Таких задач на КЕГЭ в последнее время не было, но они появились в сборнике ФИПИ-2025, да ещё с большой длиной стороны (это отбило желание решать вручную). Нам повезло, ученики пришли с геометрии и утверждали, что "углы надо уметь считать...." и пришло очевидное решение

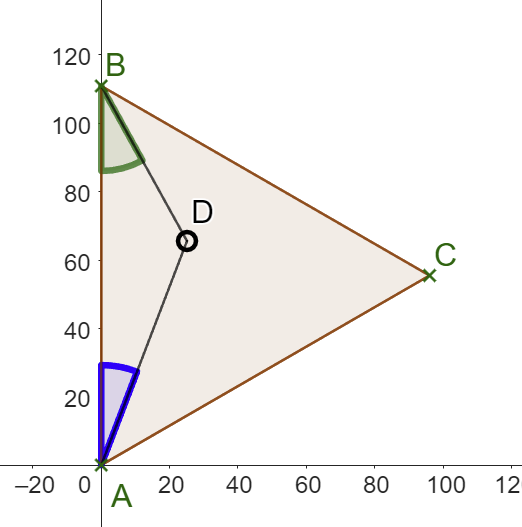
Точка D внутри треугольника ABC тогда и только тогда, когда углы DBA и DAB меньше 60 градусов, или тангенсы этих углов меньше тангенса 60
Теперь решение элементарное: пусть D = (x, y), B = (0, a). Тангенс угла DAB = x / y, а тангенс угла DBA = x /(a-y) 

Черепашка рисует шестиугольник  А можно ли аналогично решить такую задачу?
Посмотрим на эскиз и поймем, что надо найти

Нетрудно понять, что все стороны, кроме AB не содержать целых точек (иначе тангенс 30 градусов был бы рациональным)
и общее число точек есть удвоенное число точек треугольника AFE и прямоугольника AEDB
Пусть |AB| = a, тогда |AE| = a*3**0,5 = b
Точек в AEDB будет (a+1)*int(b)
В треугольнике AFE найдем аналогично рассмотренному